Unsupervised Representation Learning for Singing Voice Separation
We present a method for learning interpretable music signal representations directly from waveform signals. Our method can be trained using unsupervised objectives and relies on the denoising auto-encoder model that uses a simple sinusoidal model as decoding functions to reconstruct the singing voice. The supplementary material focuses on three “qualitative” aspects:
- Audio examples of reconstructed music signals
- Visual examples of the representation
- Visual examples of frequency responses
Audio examples
Randomly sampled mixture (mix) and singing voice (vox) segments of 3 seconds, from the test sub-set.
| Example | Input | Reconstructed |
|---|---|---|
| Mix Ex. 1 | ||
| Vox Ex. 1 | ||
| Mix Ex. 2 | ||
| Vox Ex. 2 | ||
| Mix Ex. 3 | ||
| Vox Ex. 3 | ||
| Mix Ex. 4 | ||
| Vox Ex. 4 | ||
| Mix Ex. 5 | ||
| Vox Ex. 5 | ||
| Mix Ex. 6 | ||
| Vox Ex. 6 | ||
| Mix Ex. 7 | ||
| Vox Ex. 7 | ||
| Mix Ex. 8 | ||
| Vox Ex. 8 | ||
| Mix Ex. 9 | ||
| Vox Ex. 9 | ||
| Mix Ex. 10 | ||
| Vox Ex. 10 | ||
| Mix Ex. 11 | ||
| Vox Ex. 11 |
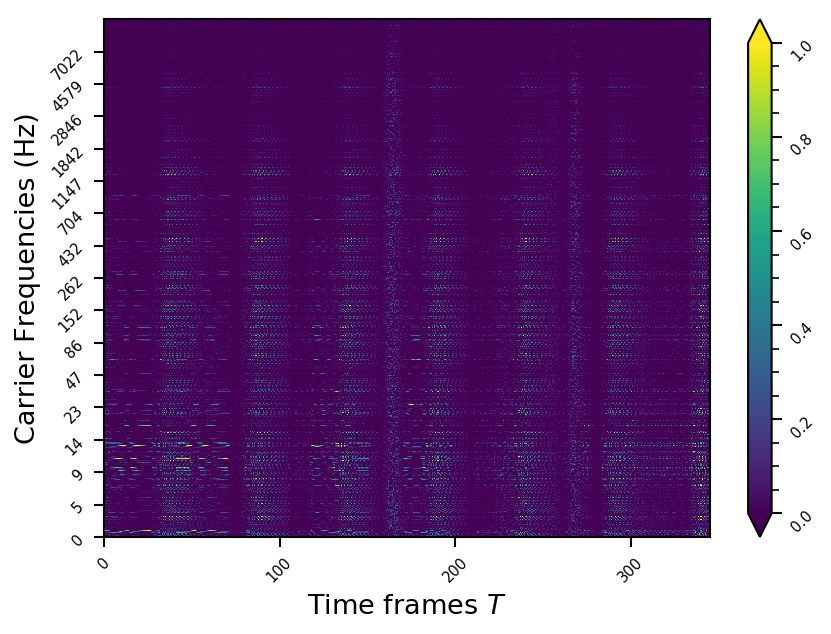
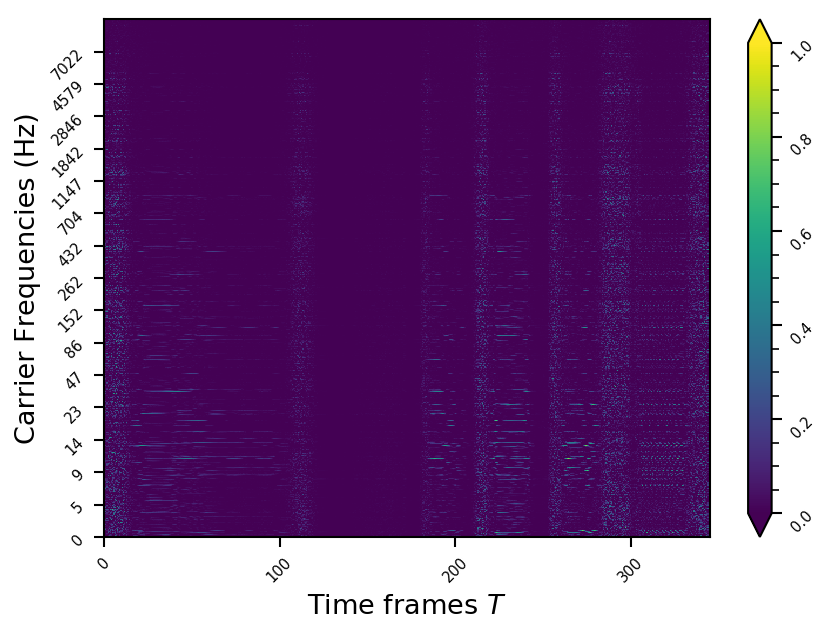
Representation examples
Example 1
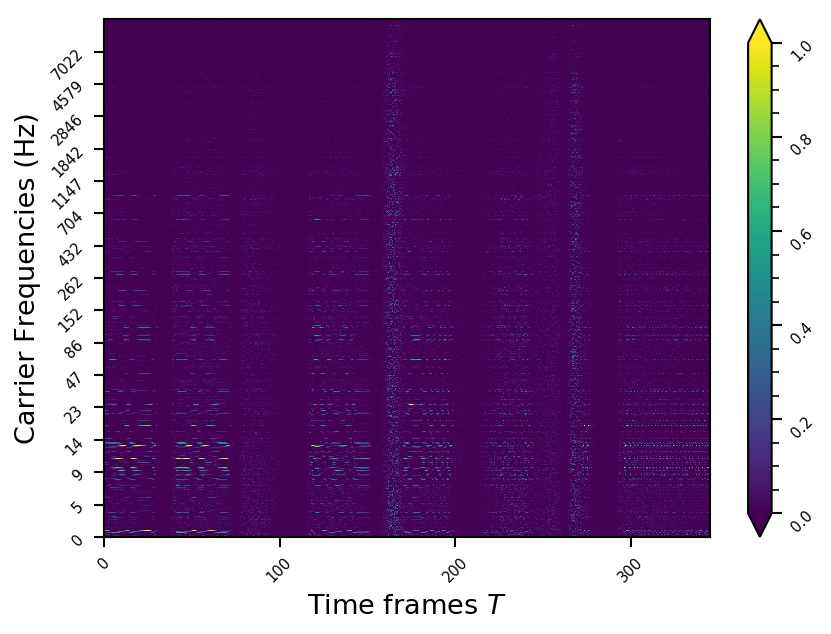
Example 2
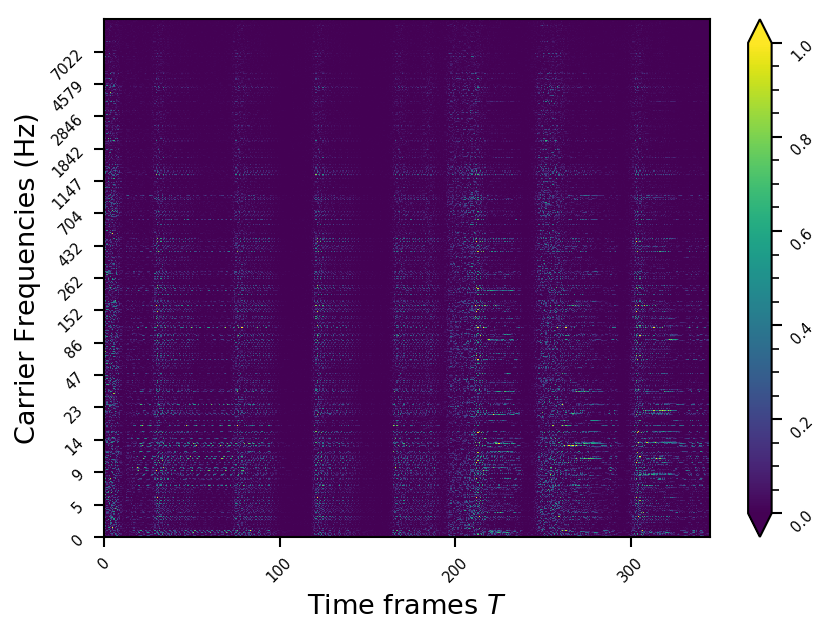

Example 3
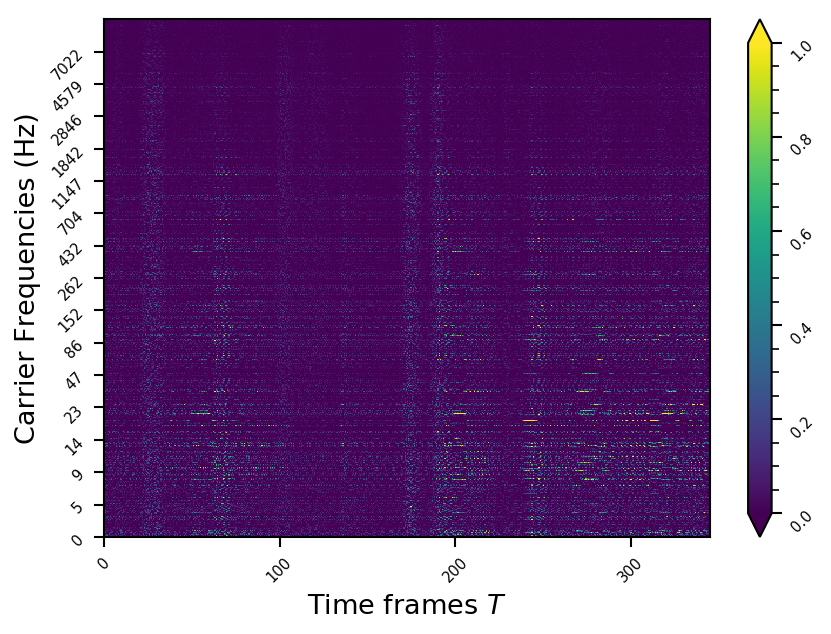
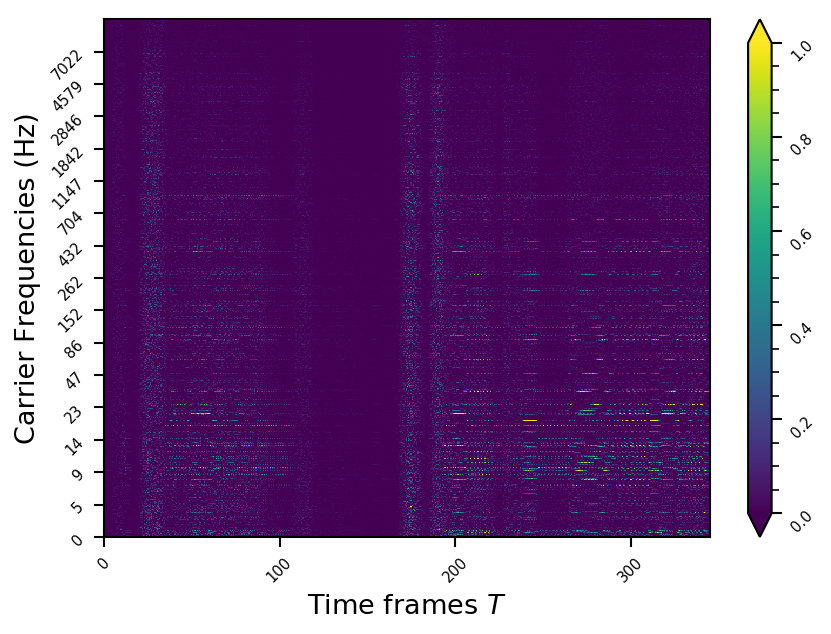
Example 4
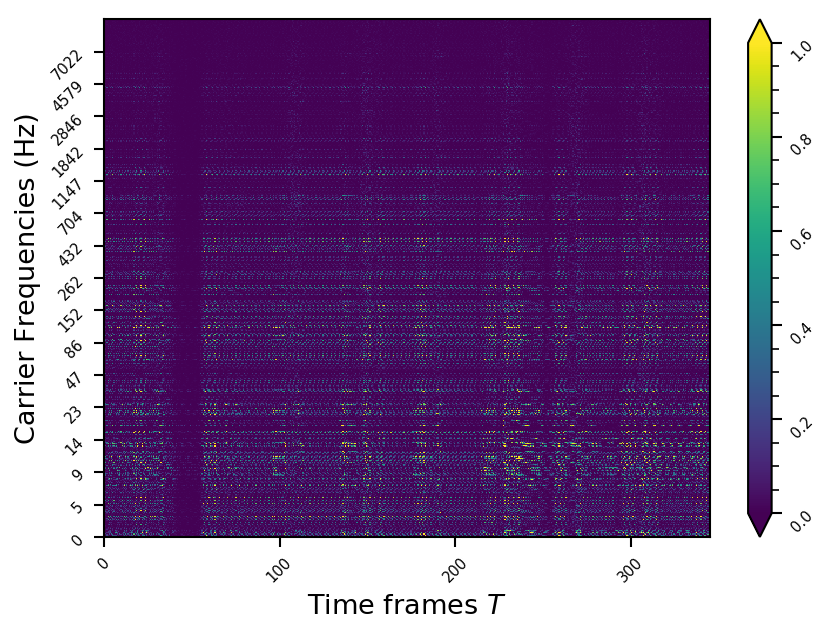

Example 5

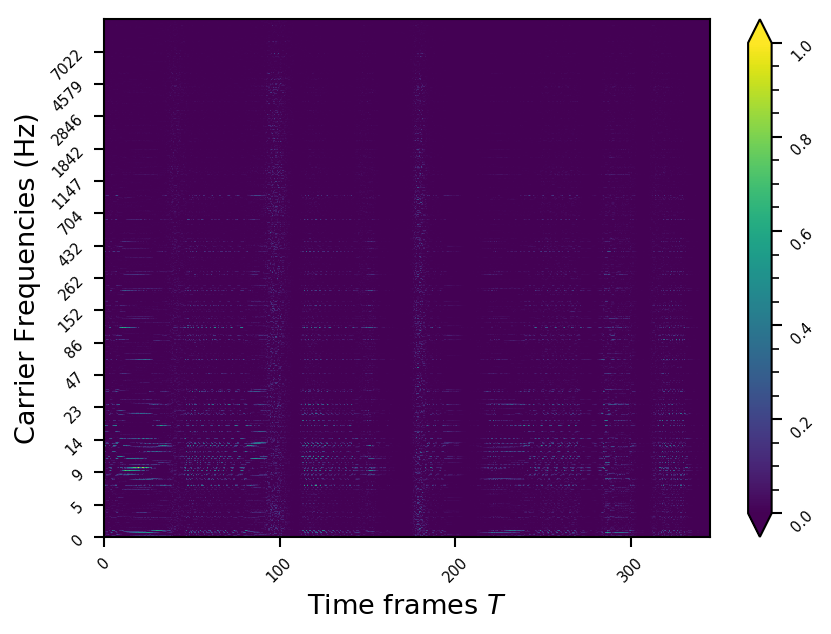
Example 6
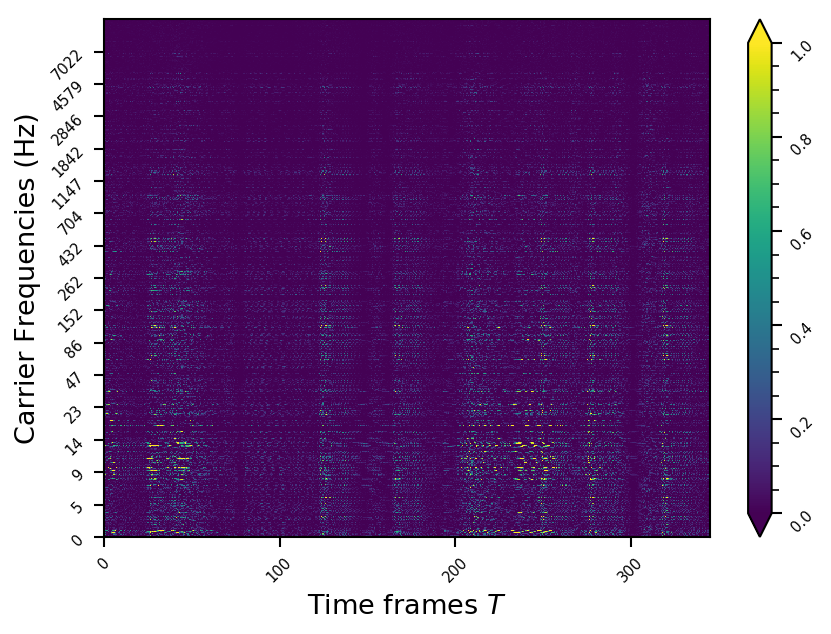
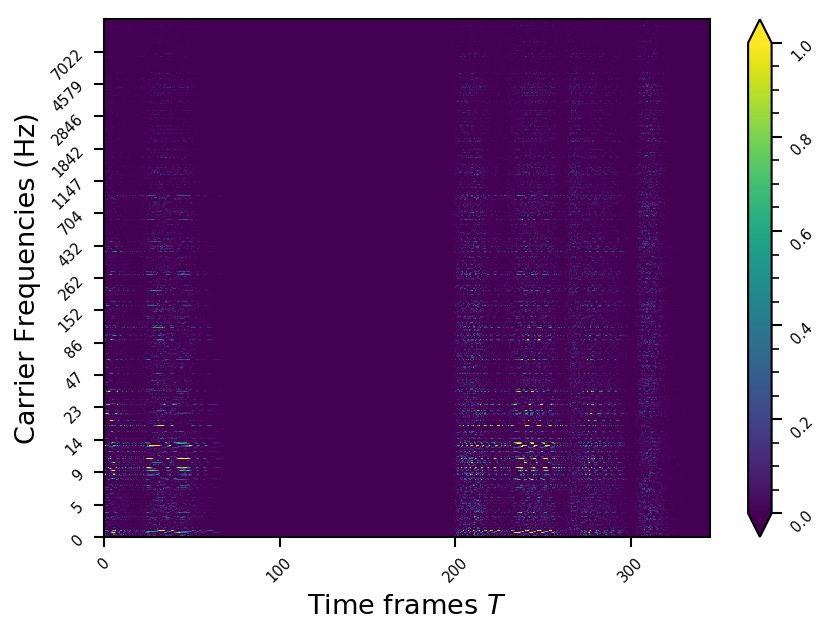
Example 7
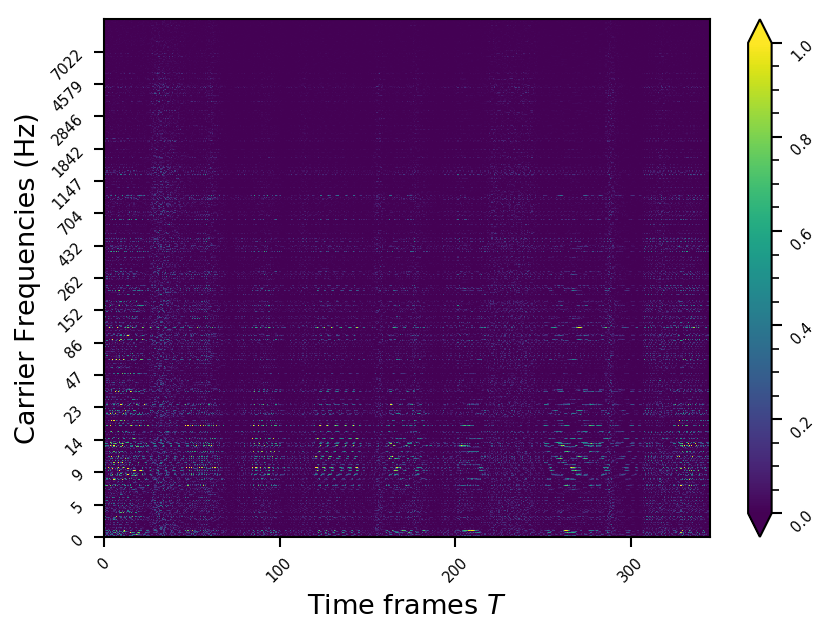

Example 8
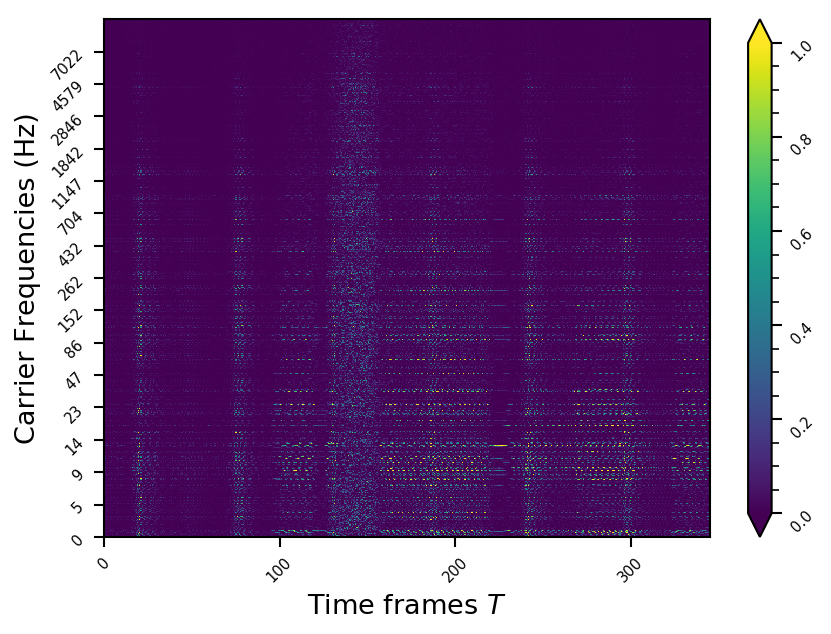
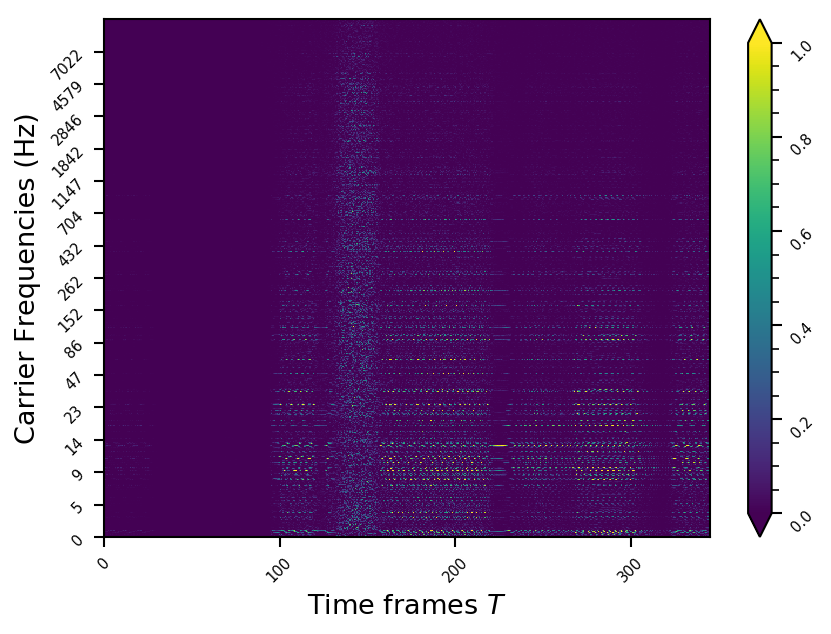
Example 9

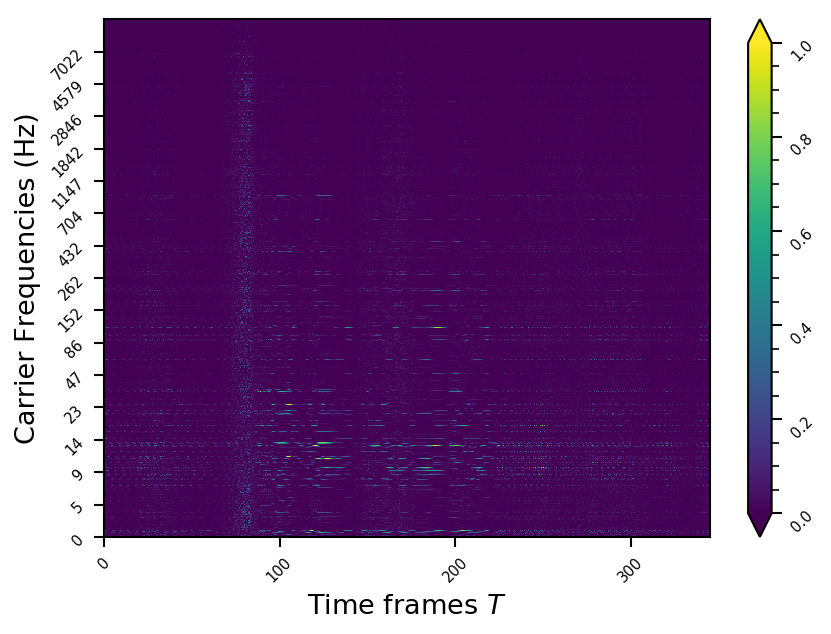
Example 10
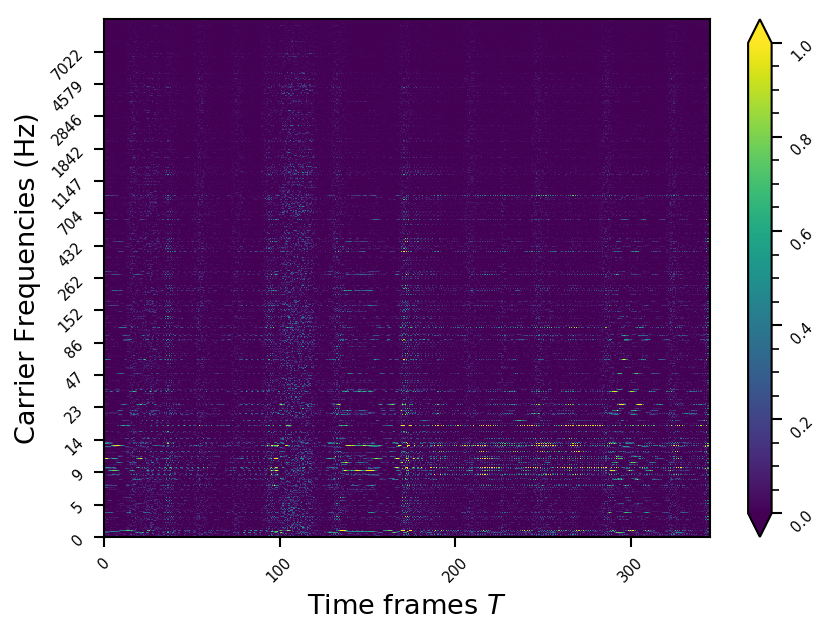
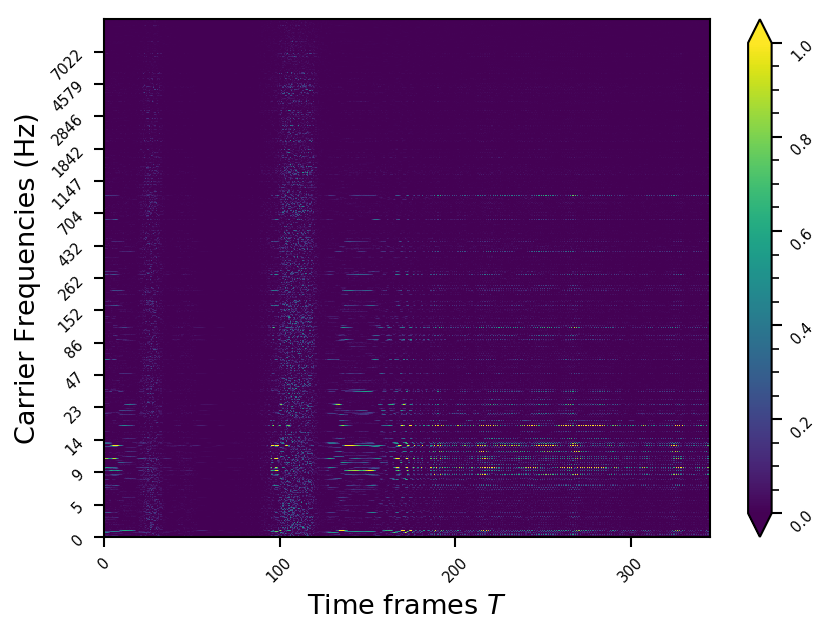
Example 11
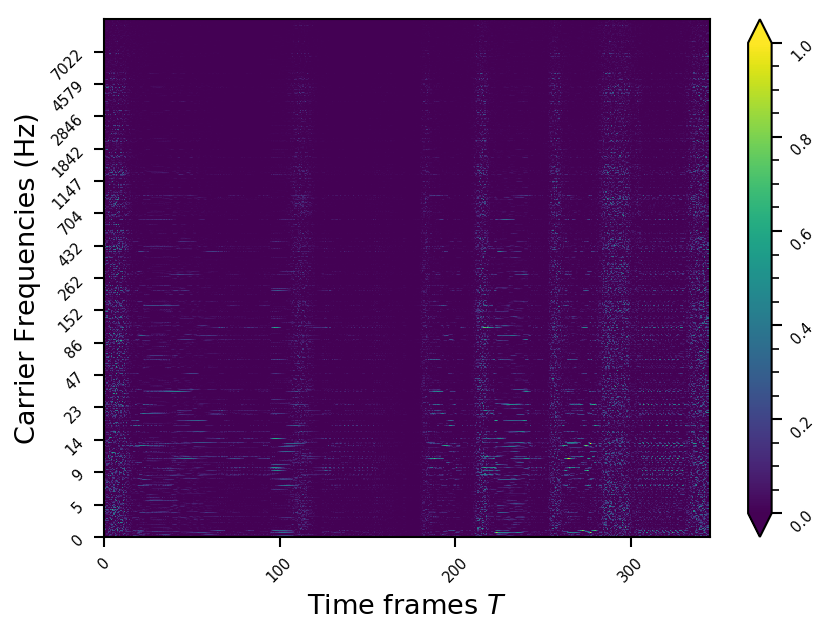
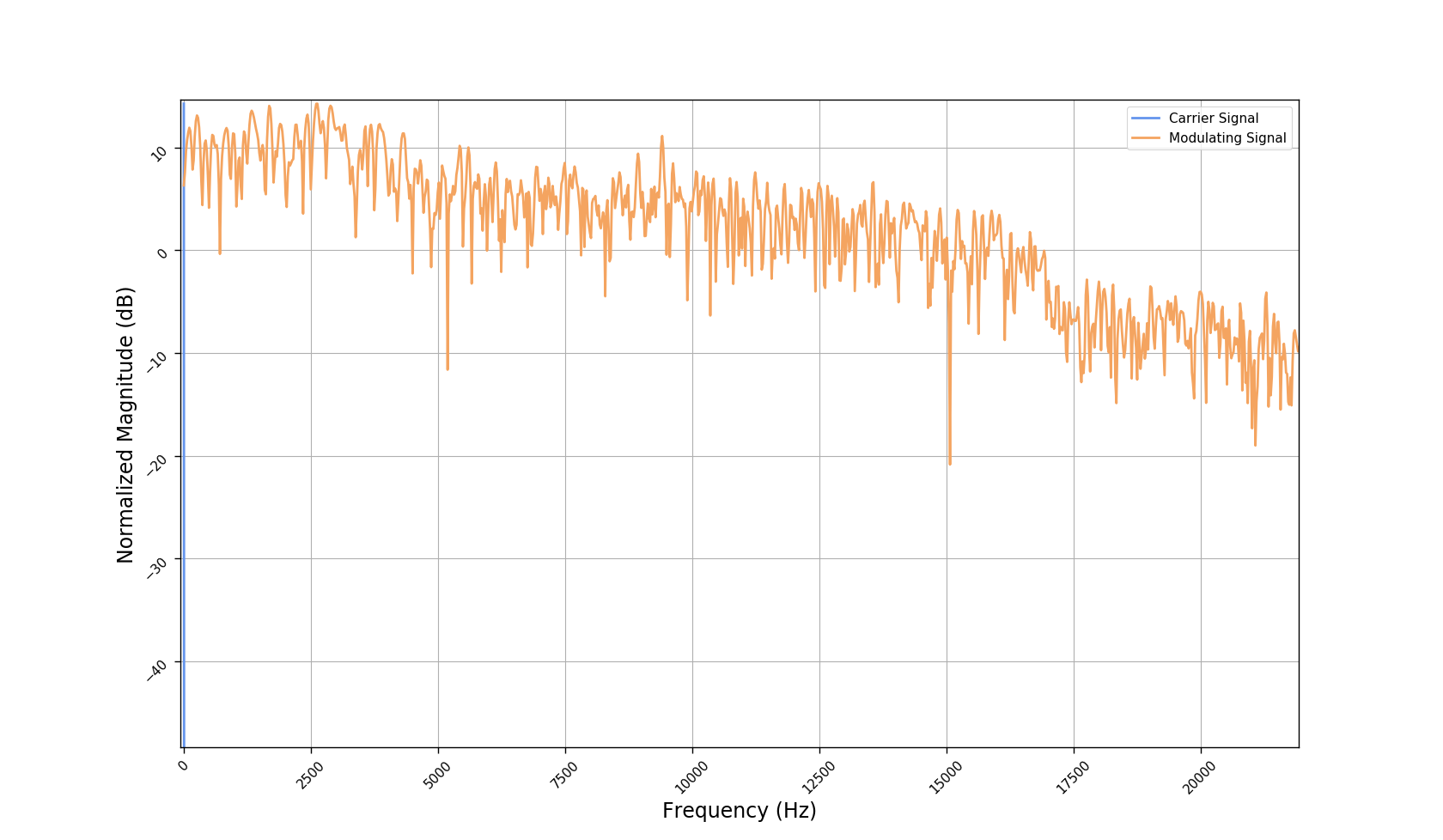
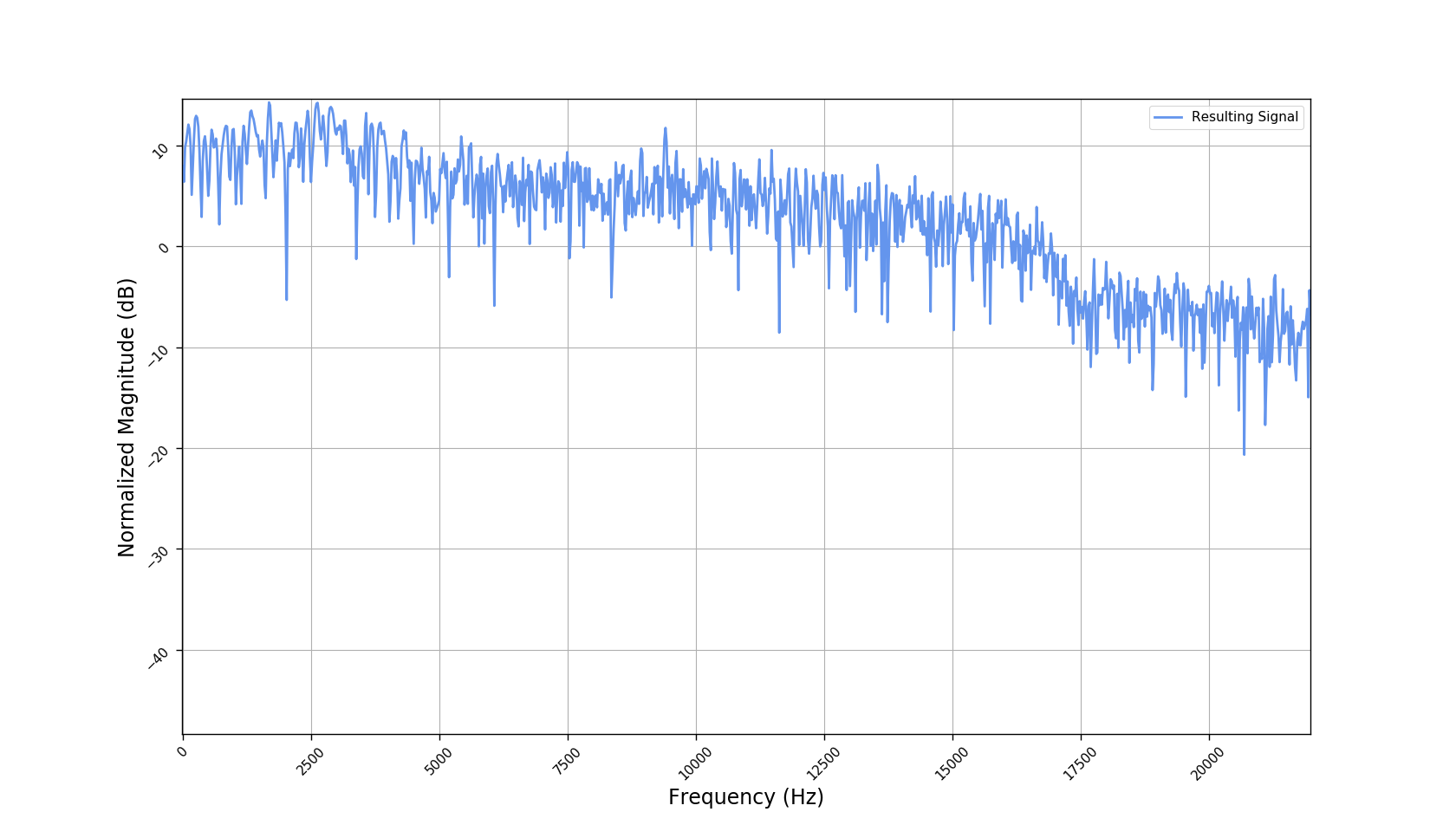
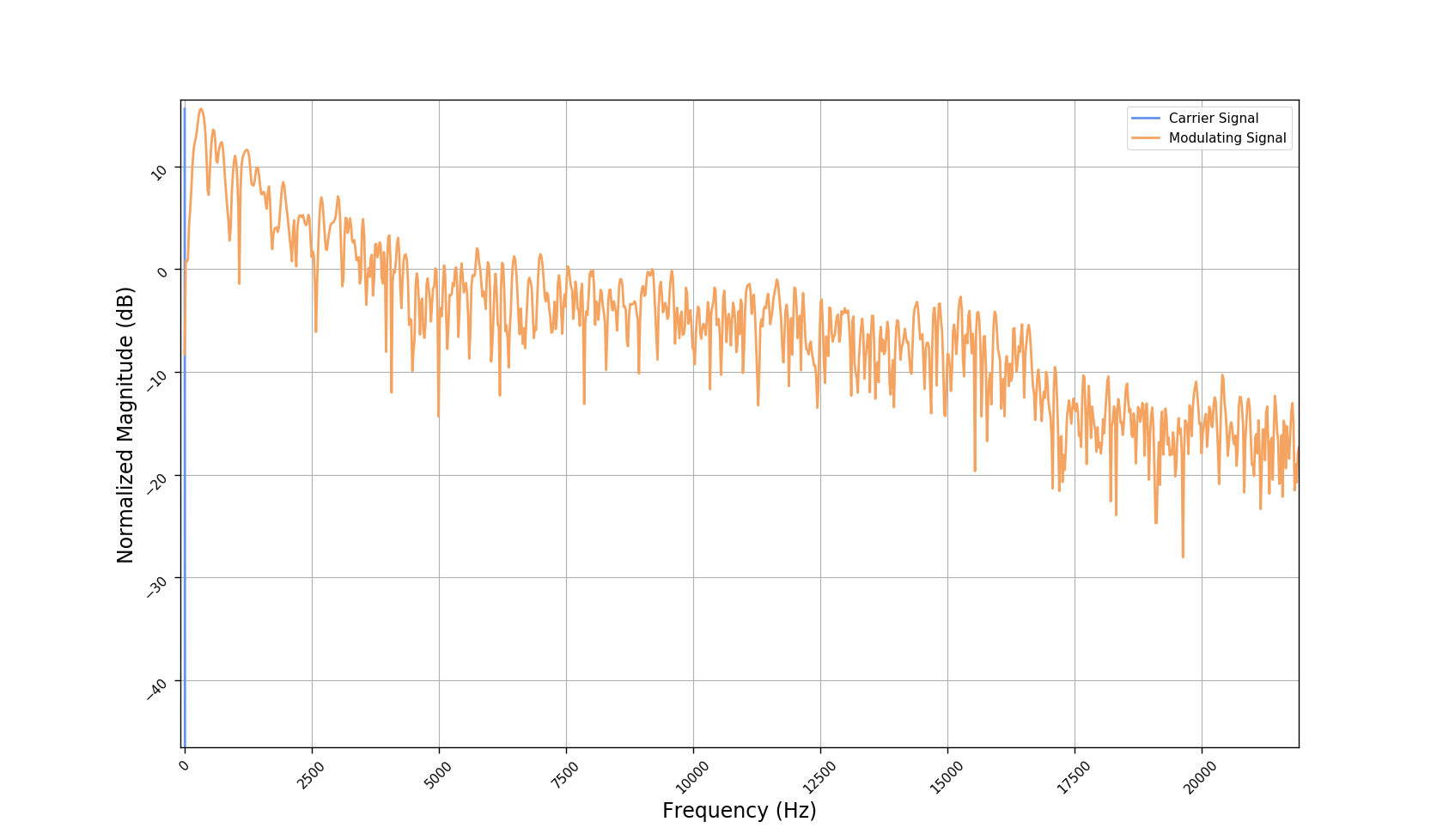
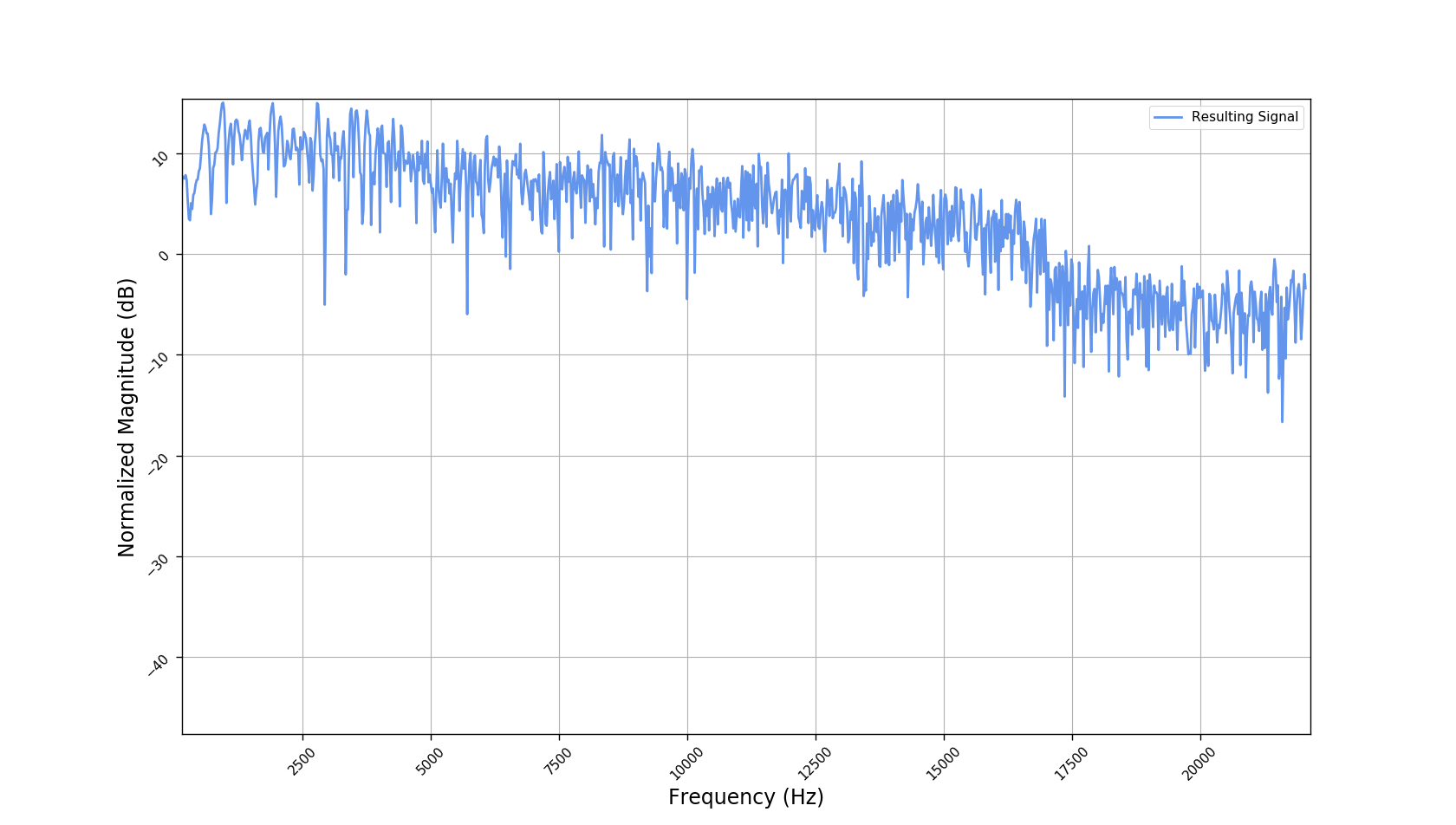
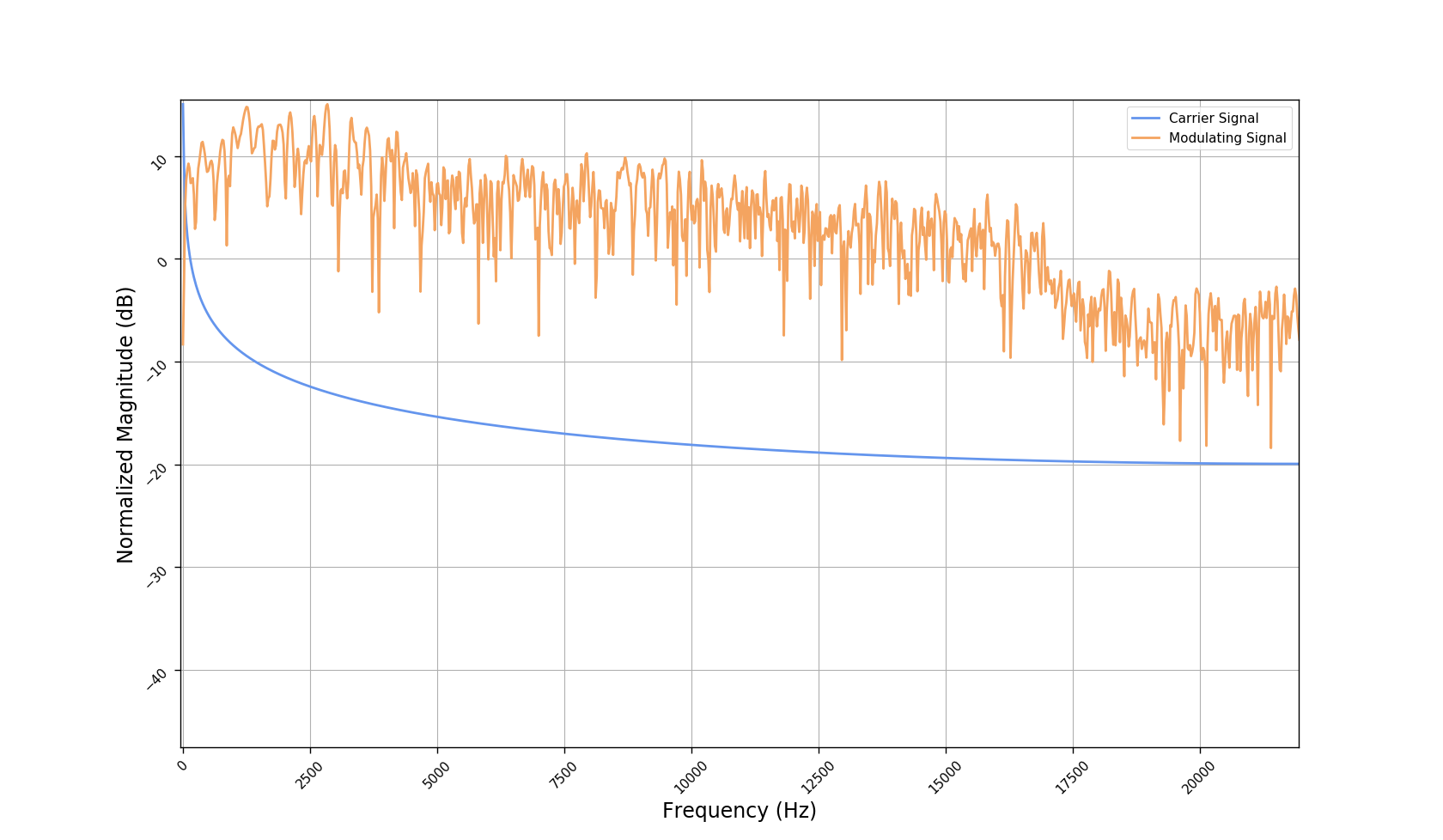
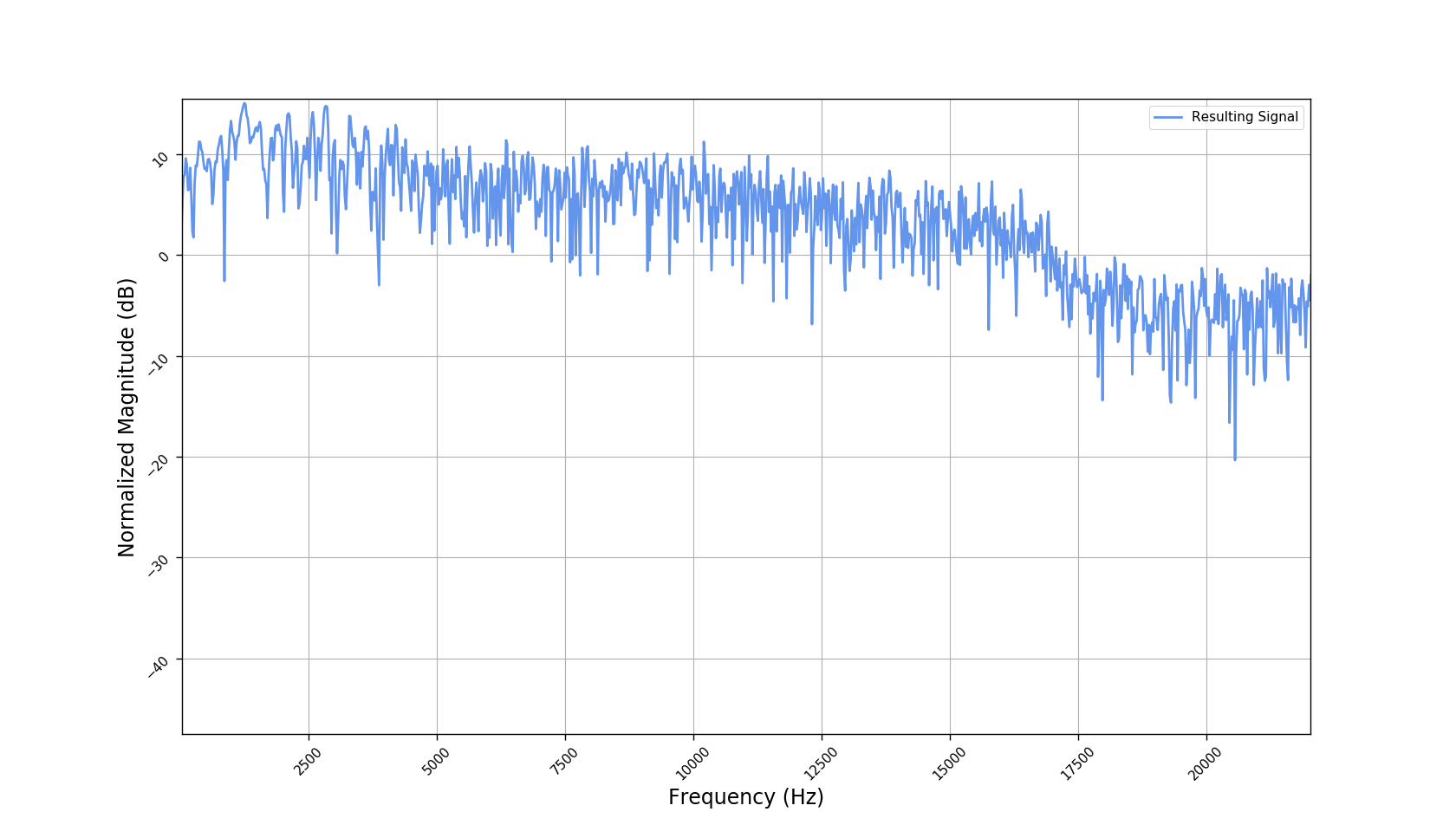
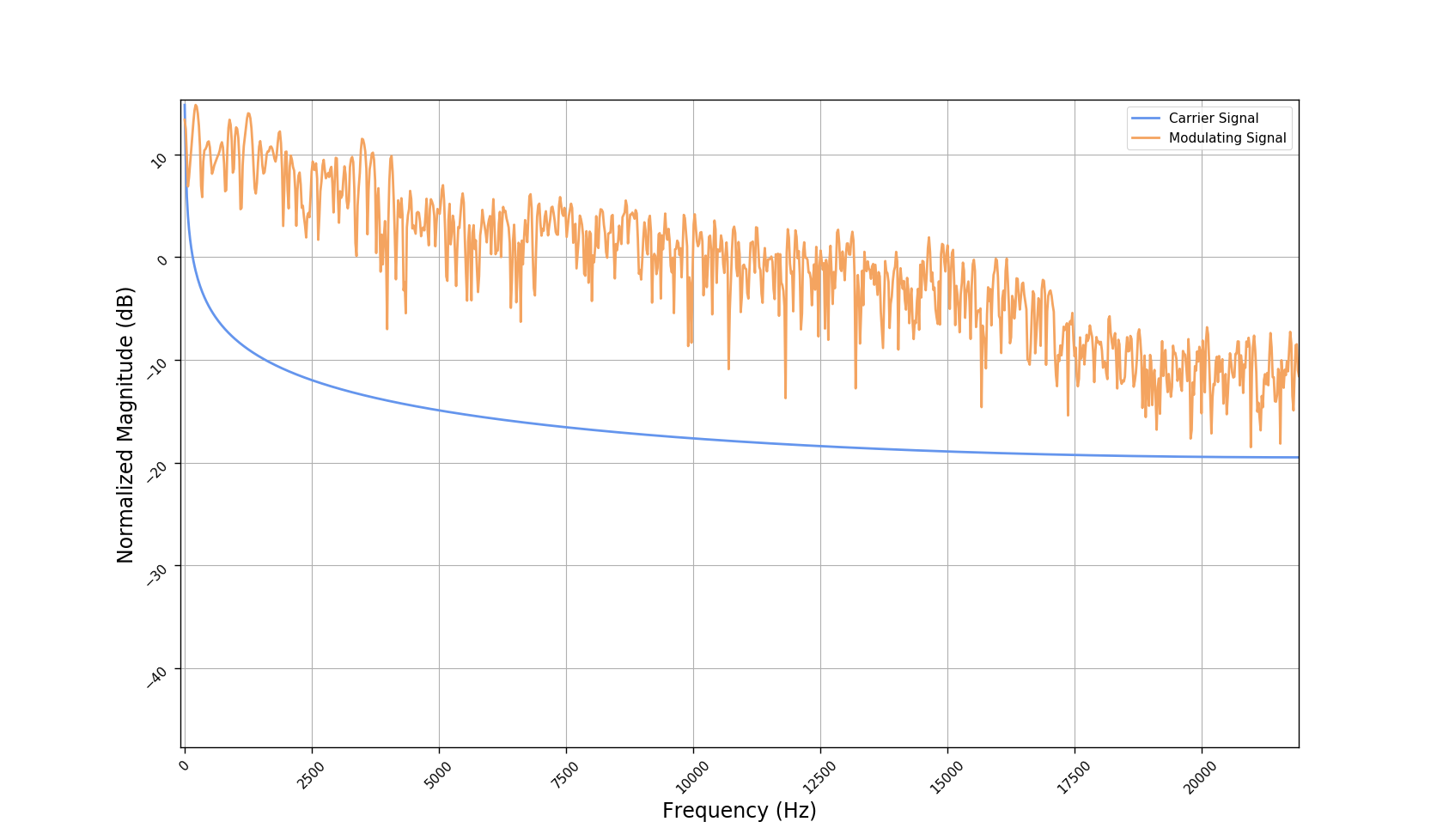
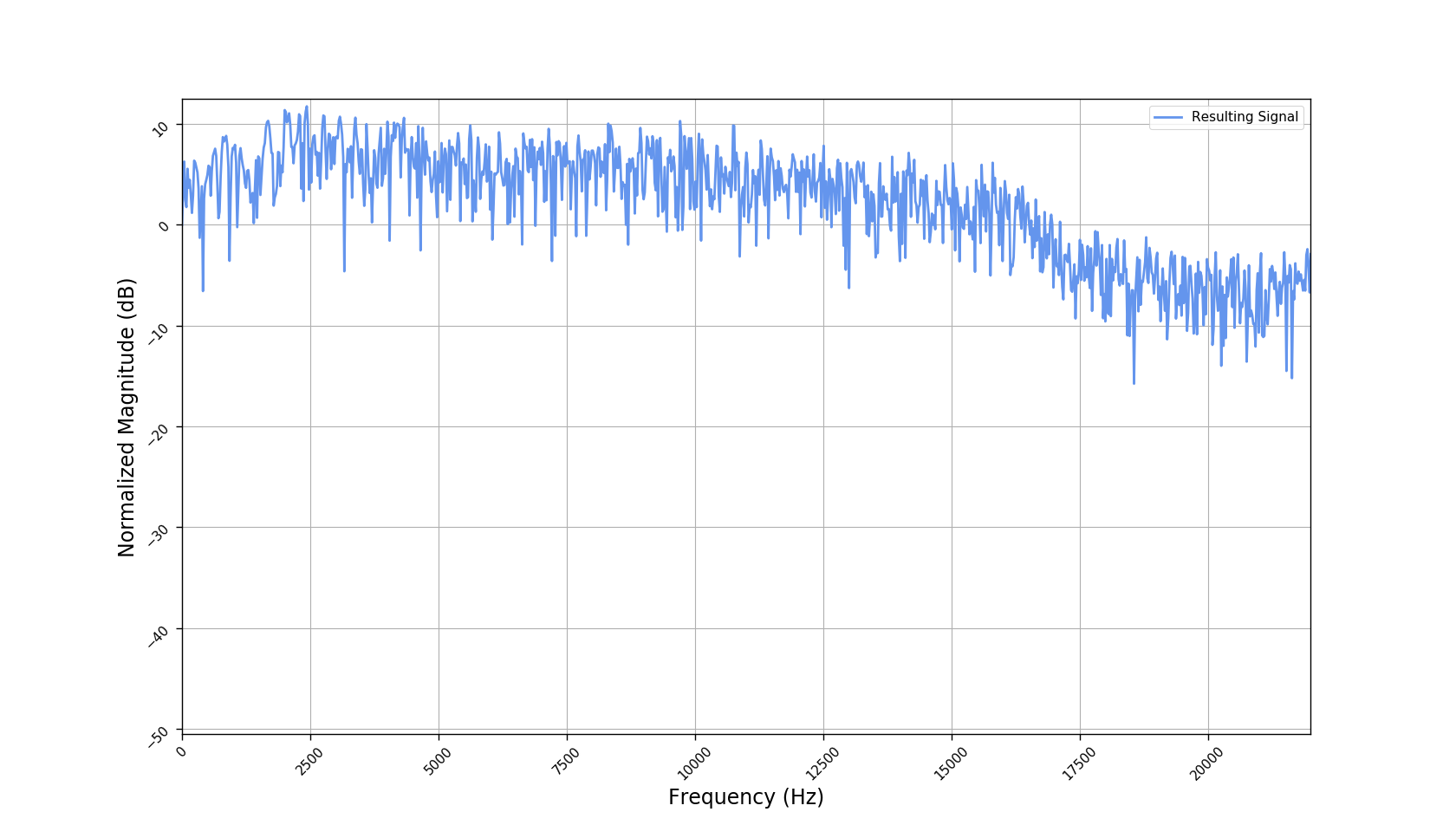
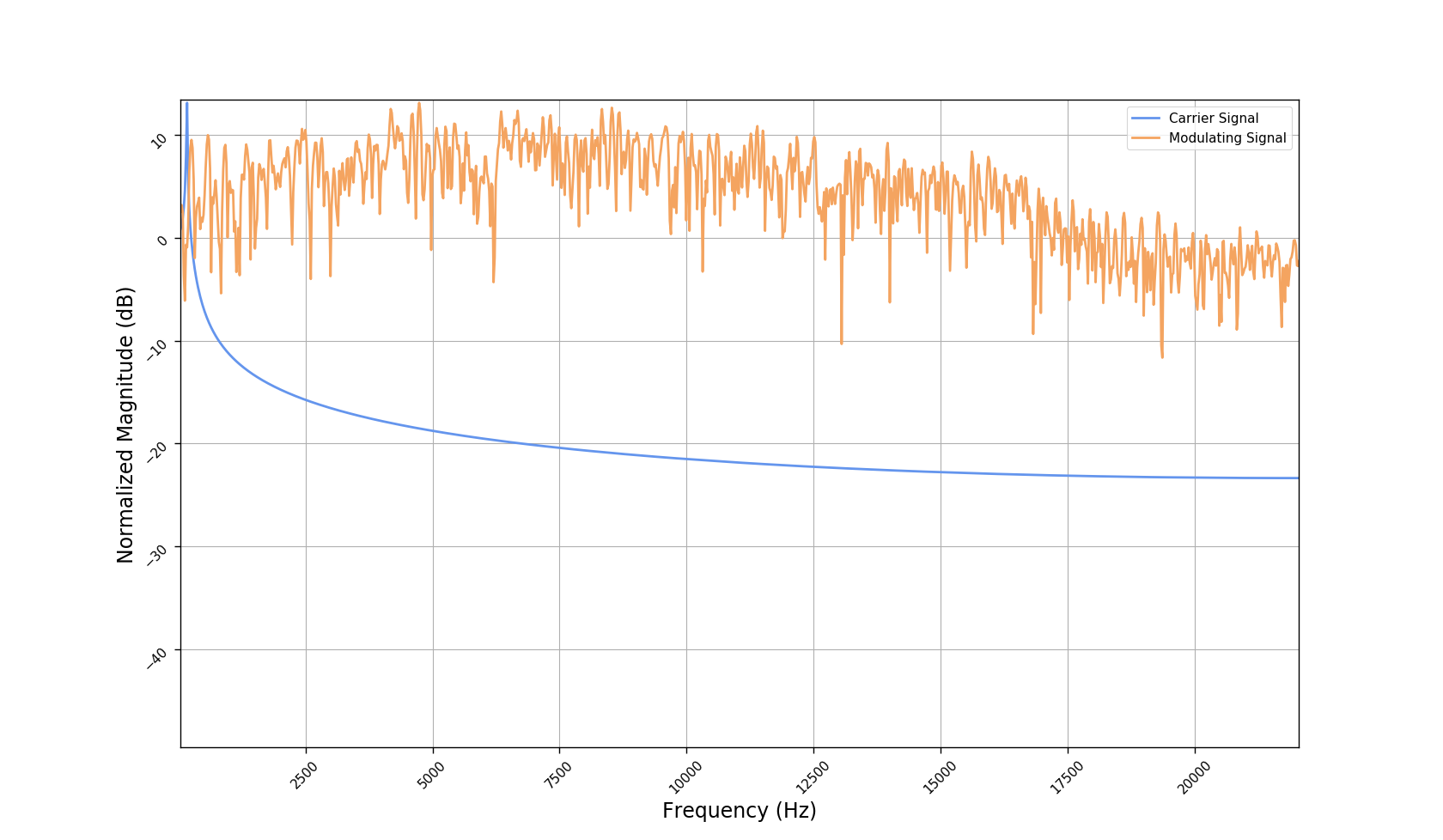
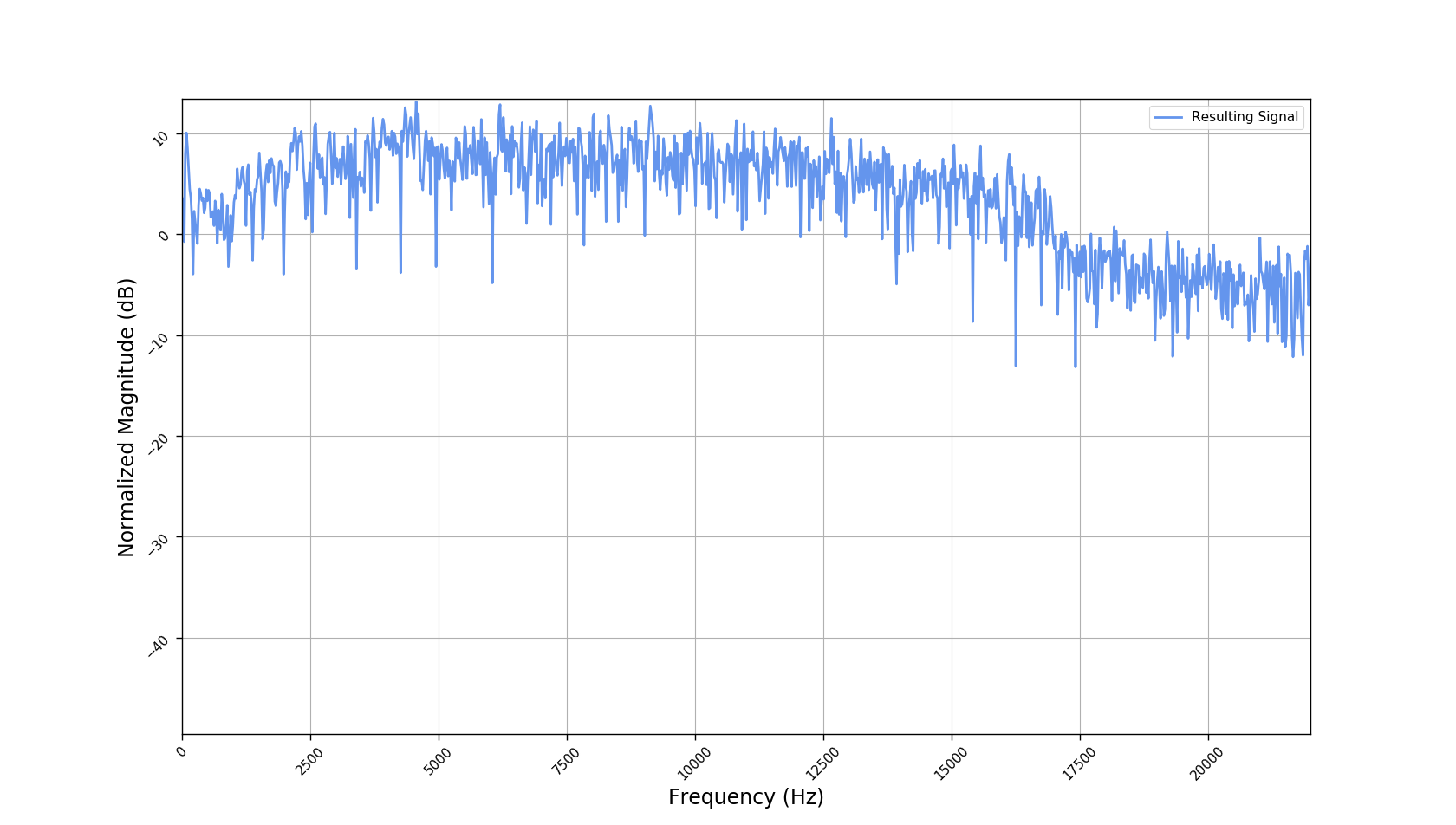
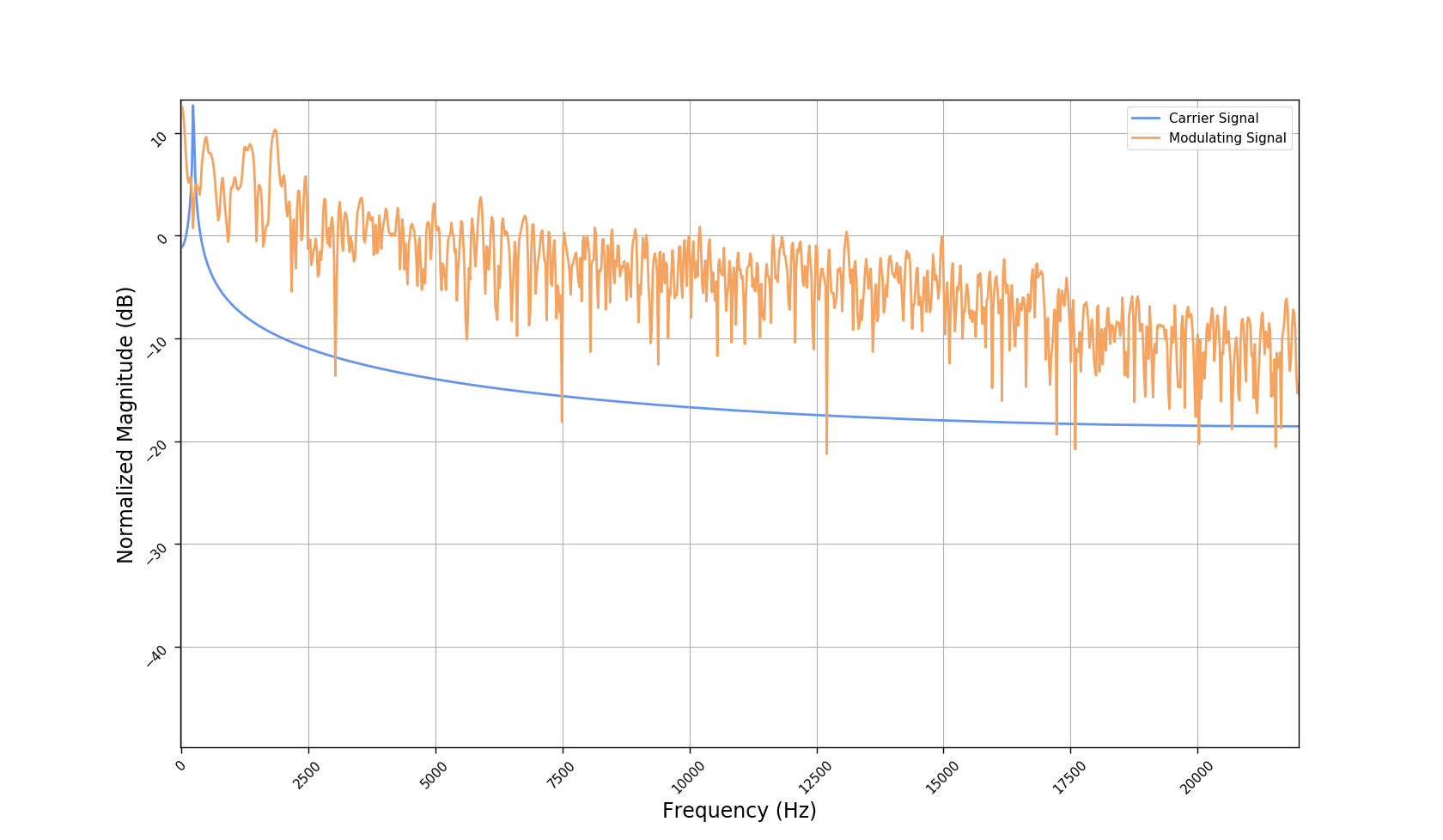
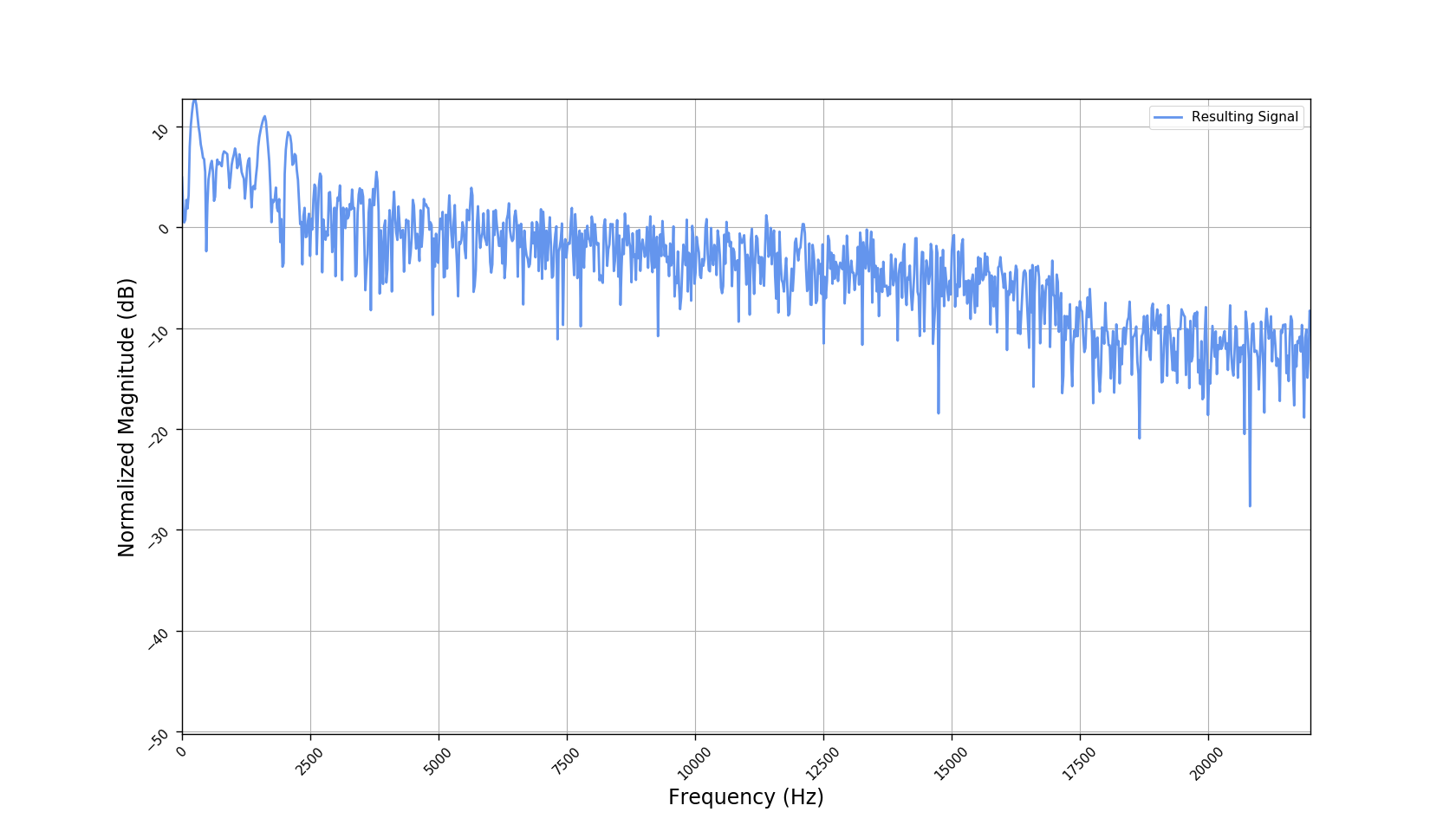
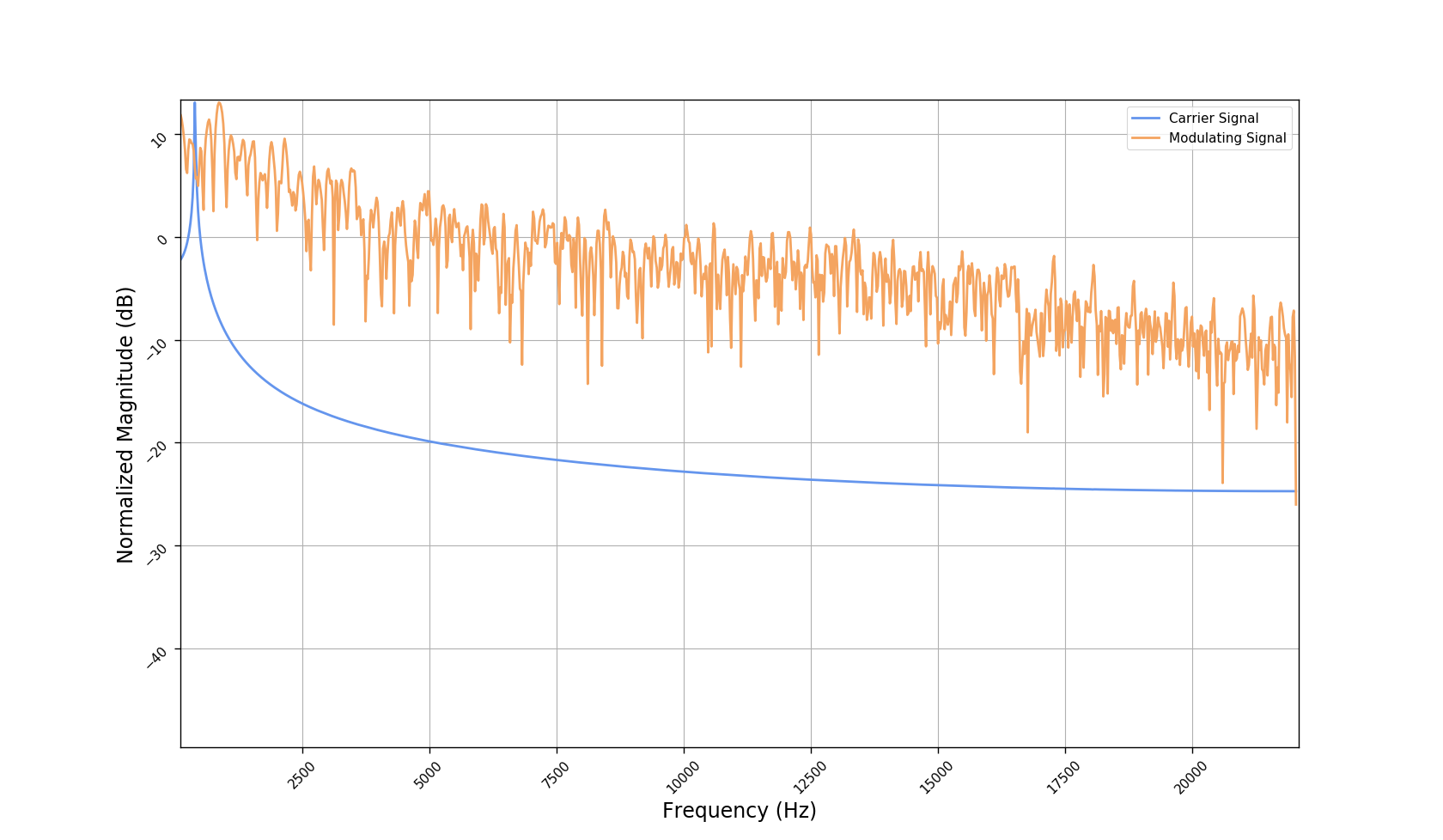
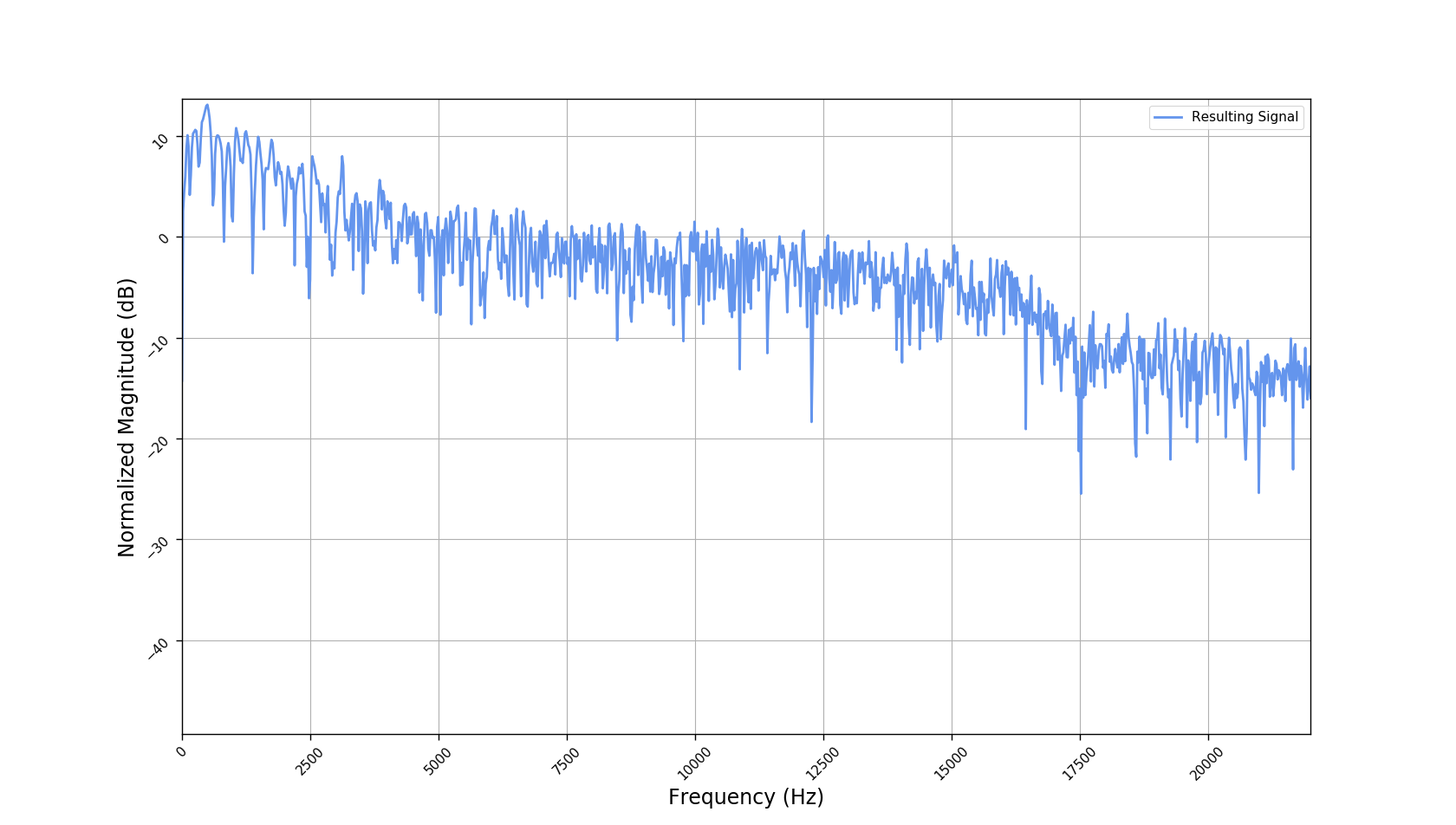
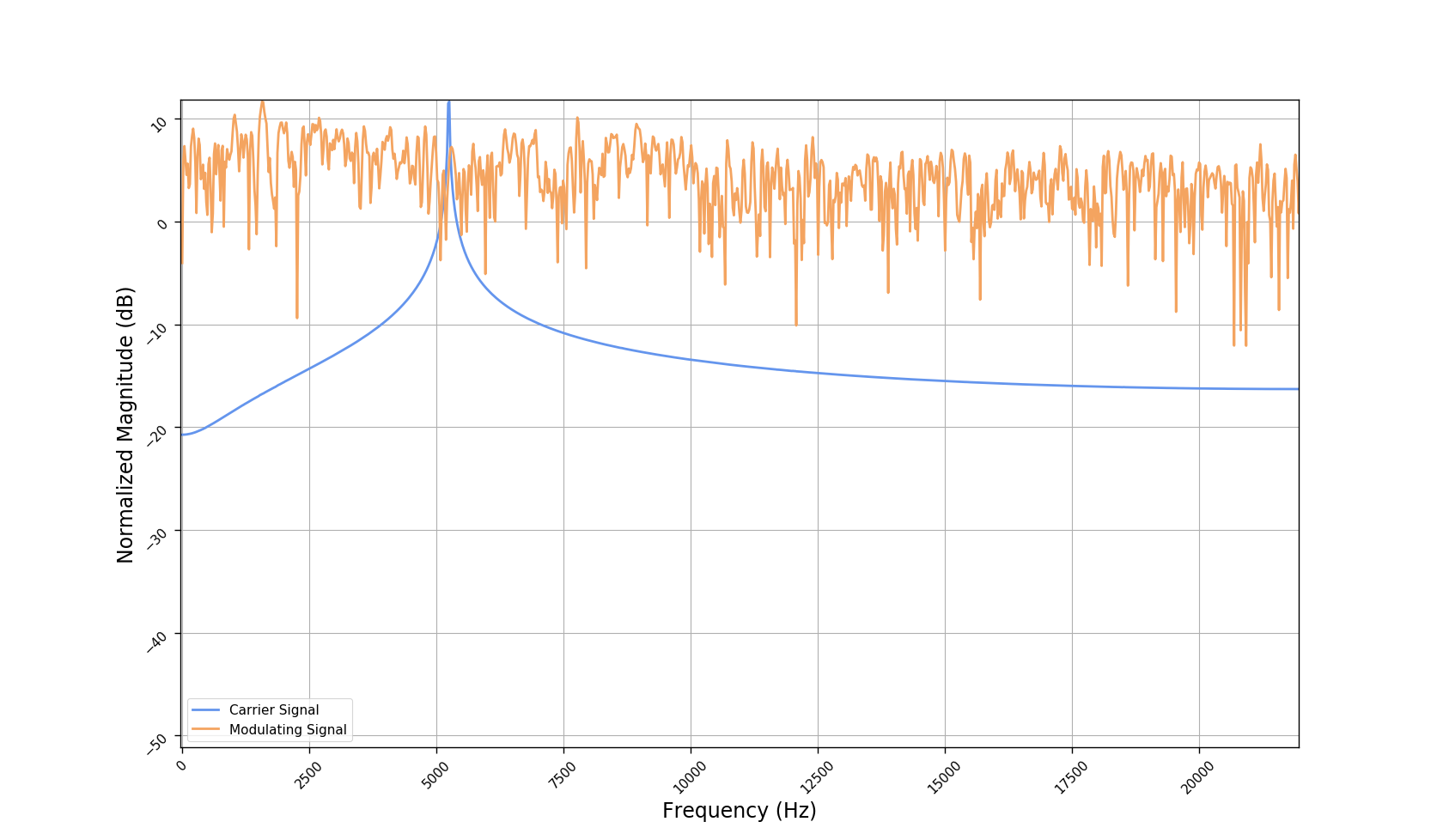
Frequency responses
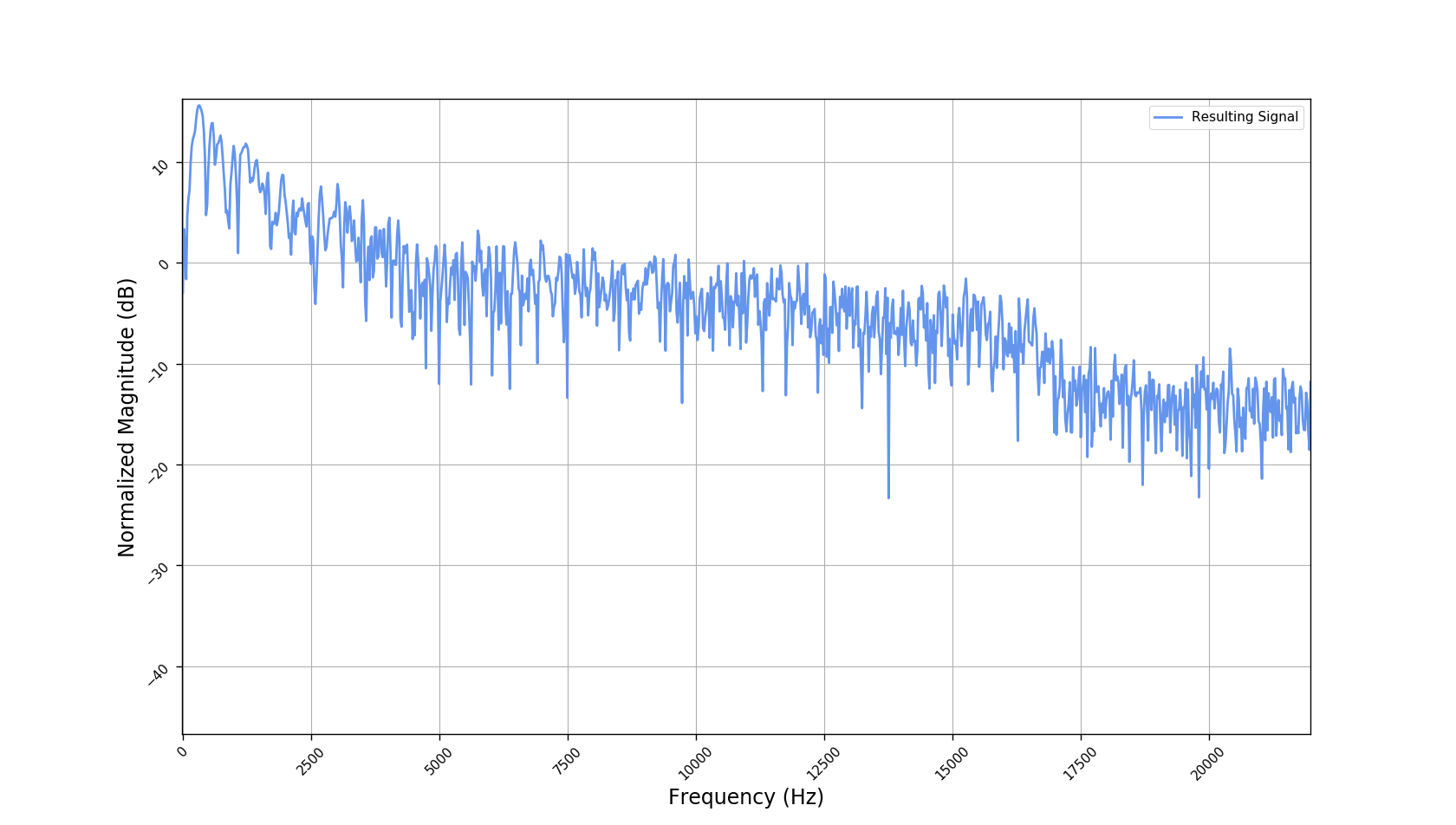
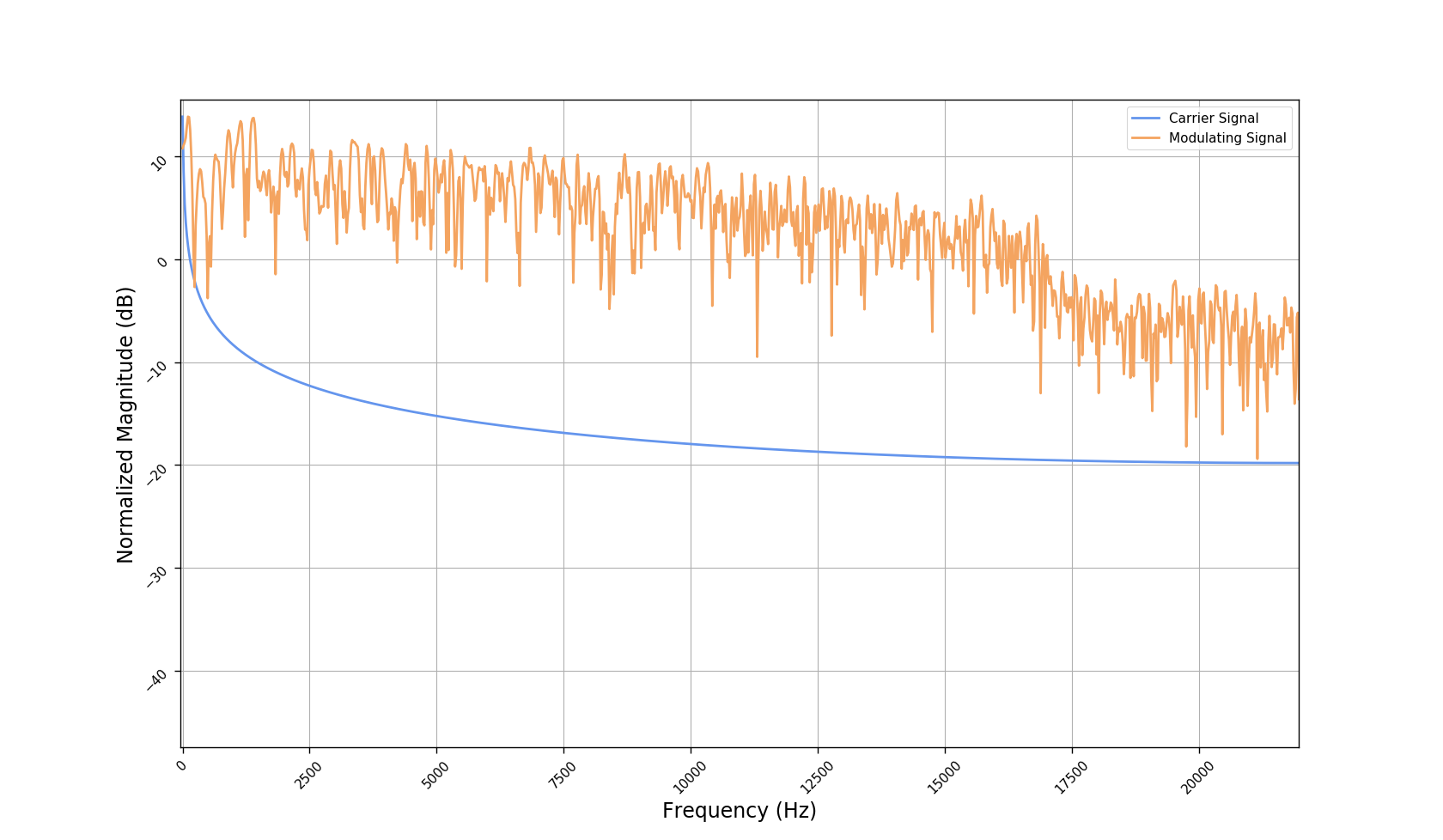
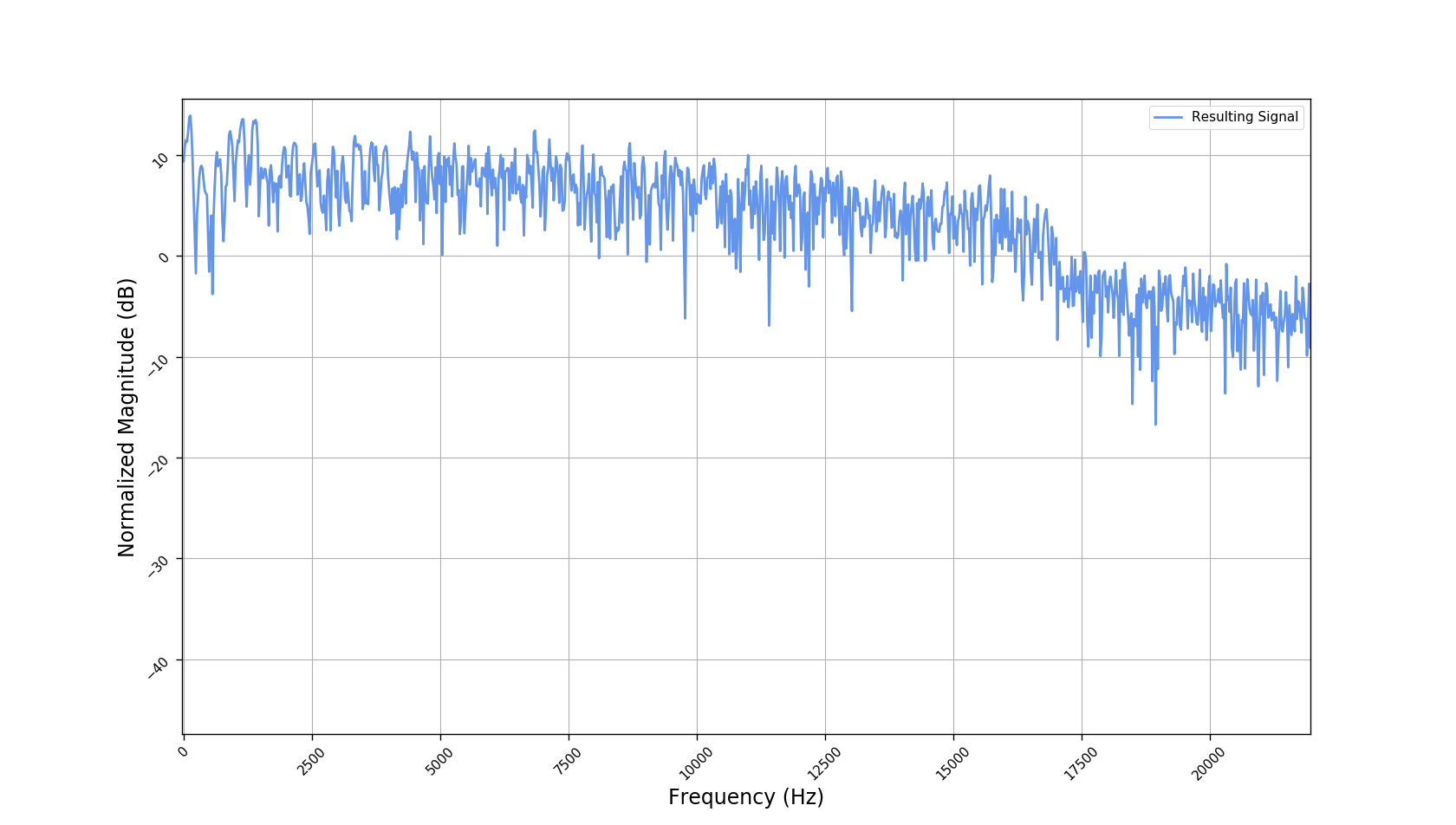
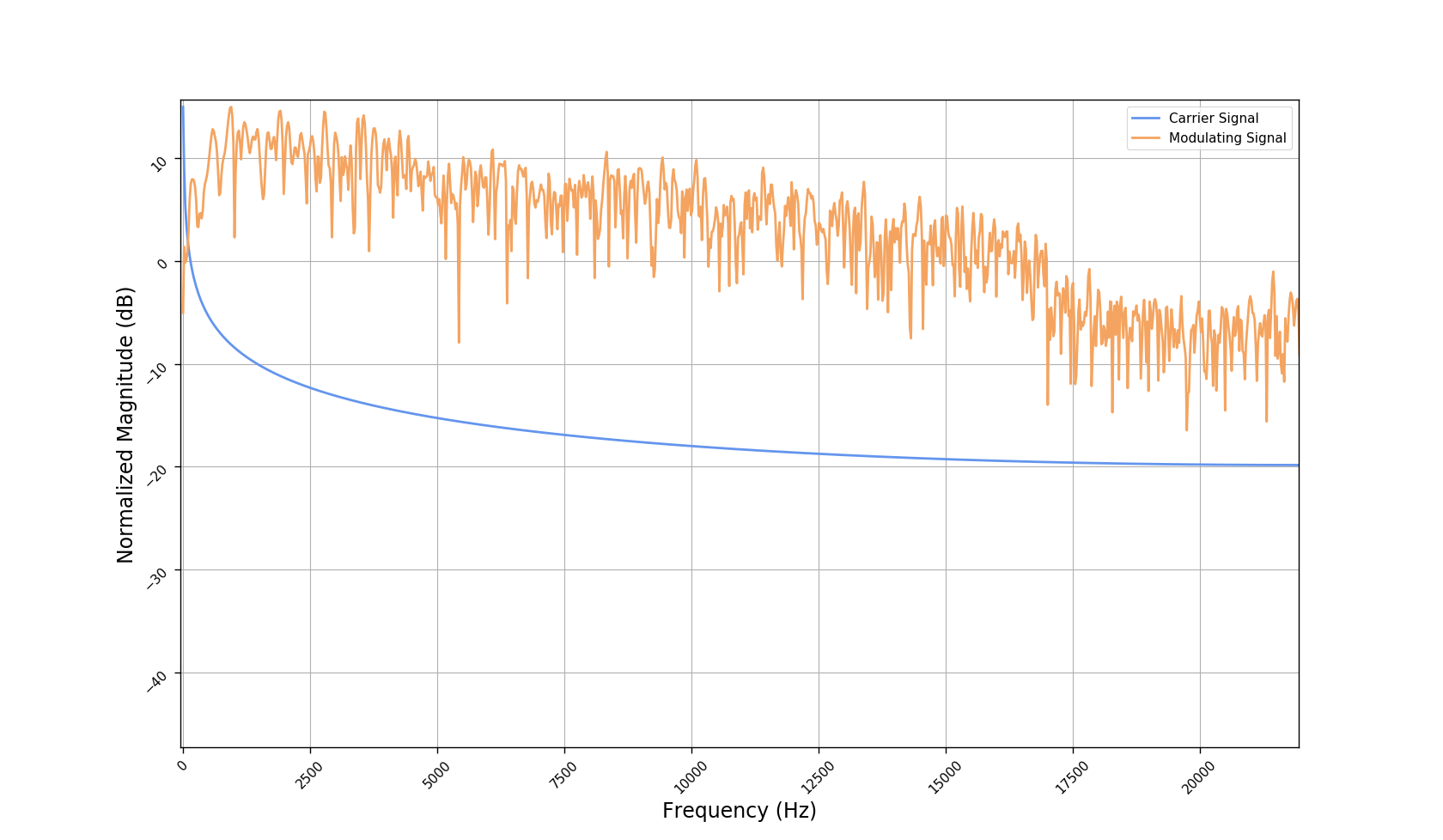
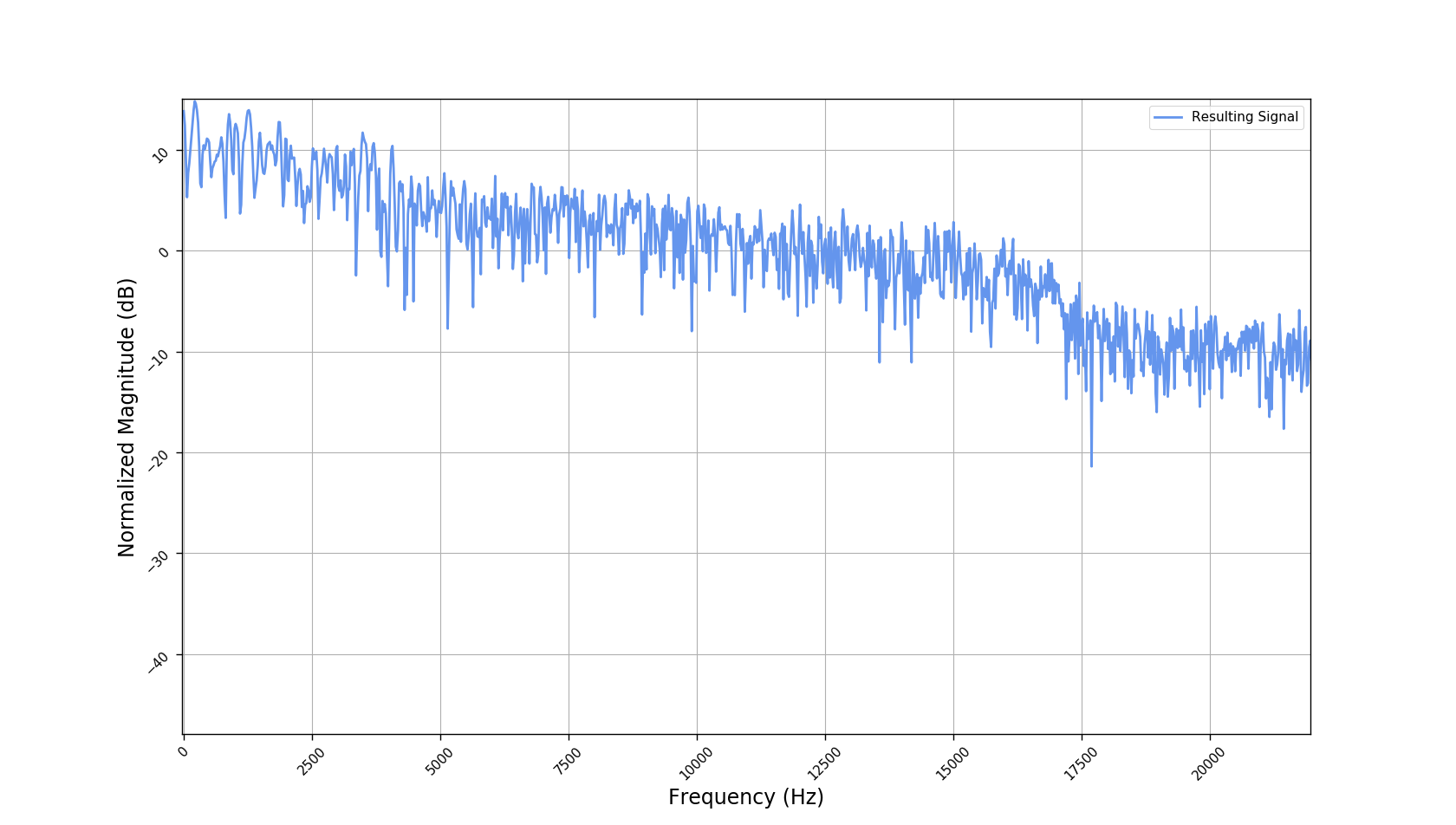
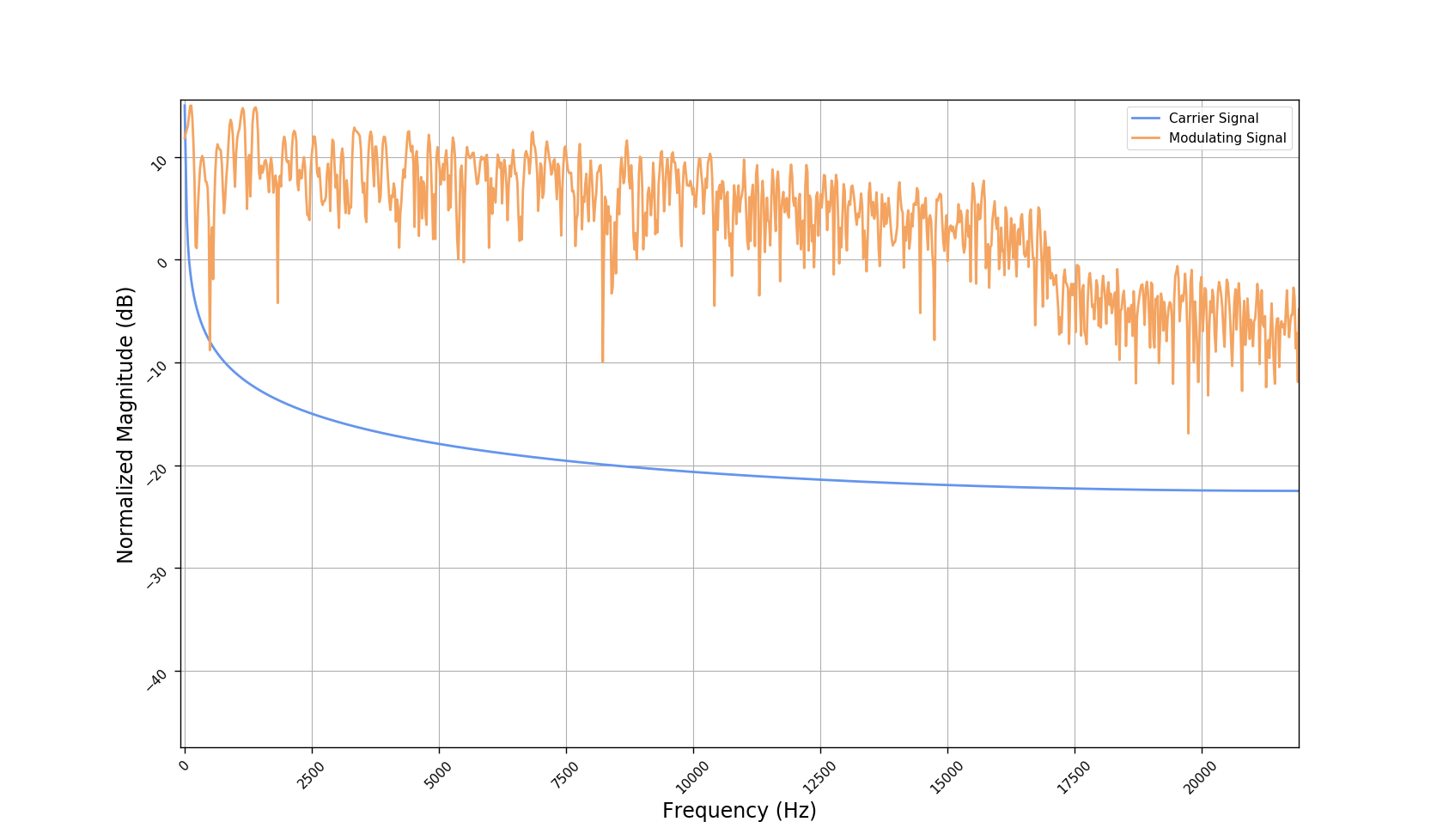
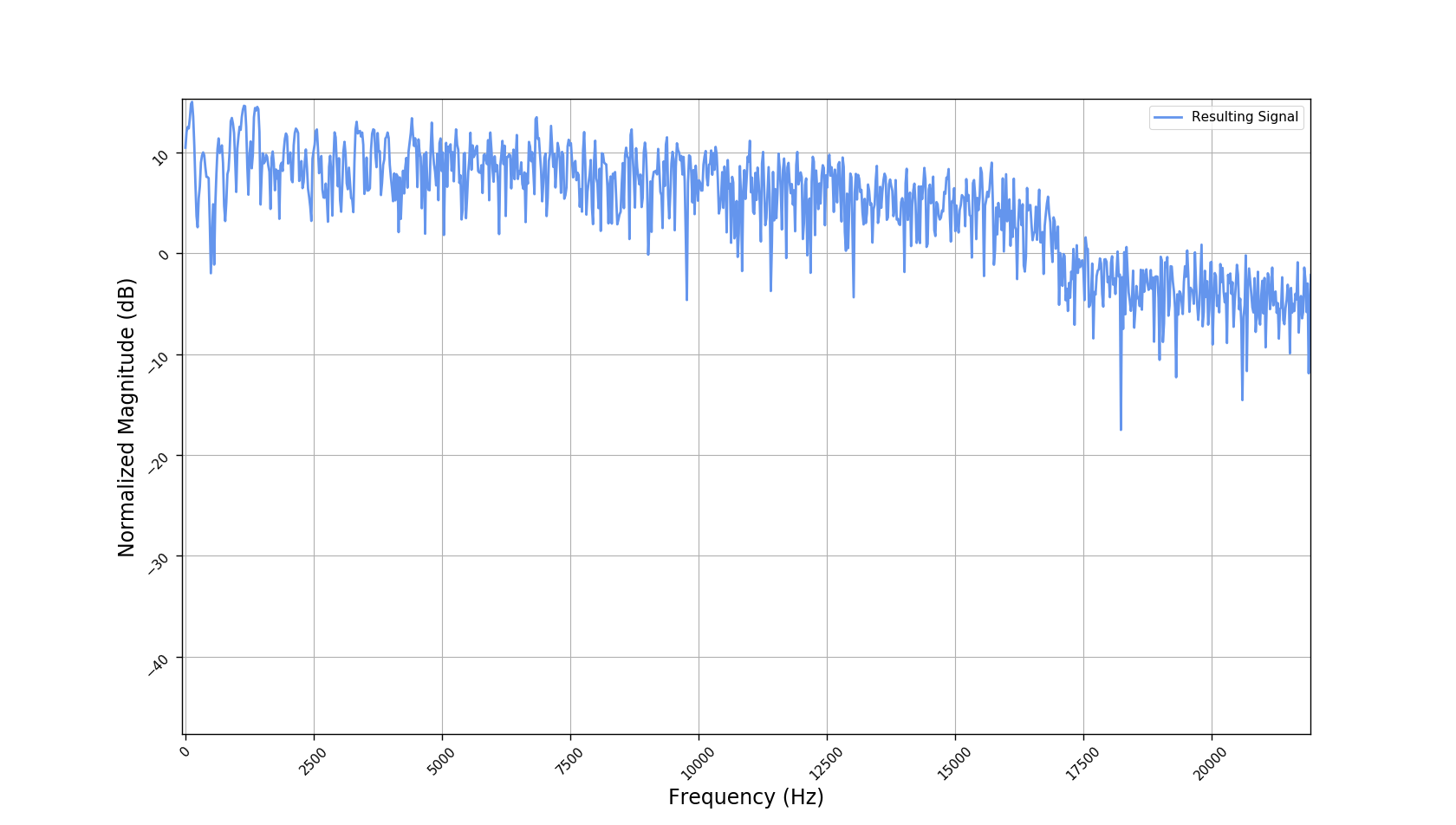
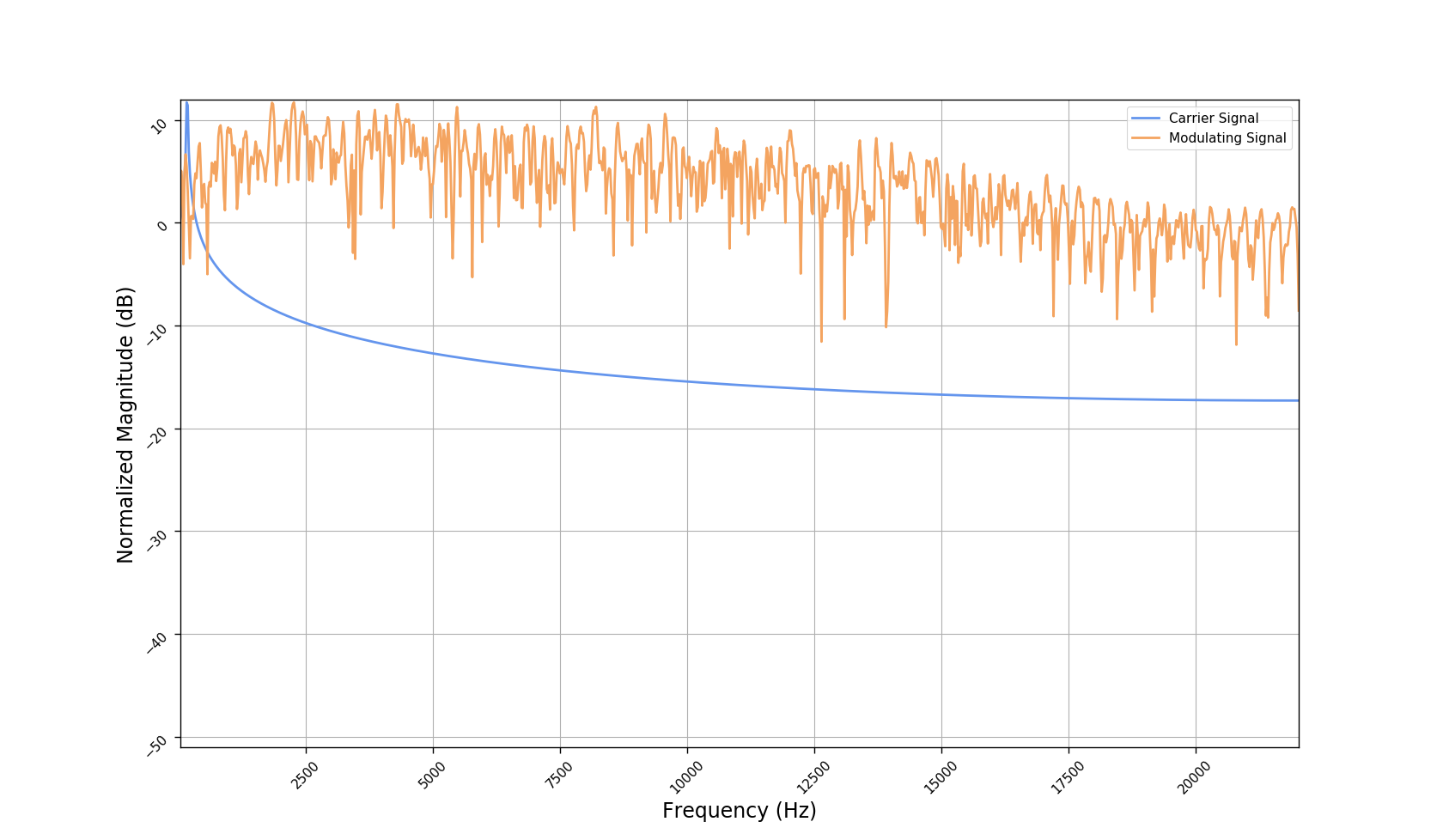
We used the best performing model, reported in our paper, and compute the discrete Fourier transform (DFT) of the resulting basis signals, that the decoder is is using. We cherry picked some the basis.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
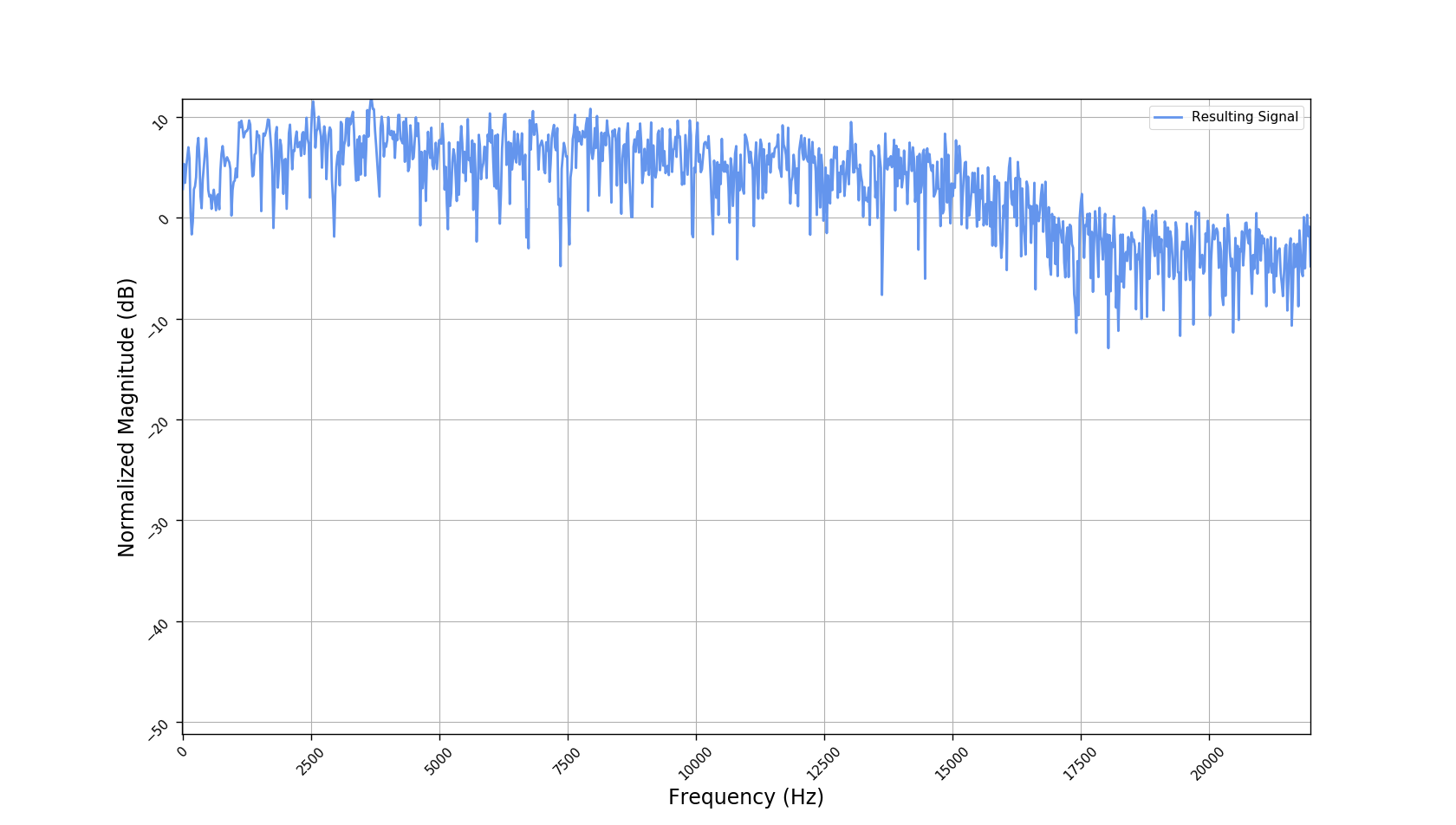 |
Observations & Take-home Messages
From the above collection of figures we could conclude the following:
- The representations using our method, are phase-free, real-valued, and are kinda like the magnitude of the short-time Fourier transform (STFT). Representation of singing voice signals can be described by “horizontal” activity, acrross time, whereas other components are scattered quasi-randomly in the representation. Therefore, further representations objectives are emerging.
- Masking, a glorified approach to music source separation, can still be applied to the above representation. However, and as seen from the frequency plots, masking a single element essentially removes much more information than a sinusoid from the analyzed signal. Subtracting representations could be more convenient.
- Our expectactions for the structure of the modulation signals, presented in the related paper, are not very far away from the realization (illustrated above). They practically offer extra fidelity parameters for reconstructing singing voice signal. Nonetheless, many basis signals are still un-structured so further examination or even inception-like re-parameterization is necessary.